
分析 (1)在中国队先输一局的情况下,中国队本场比赛获胜的可能性有两种:连胜3局或前3局两胜1负,第五局胜,由此能求出在中国队先输一局的情况下,中国队本场比赛获胜的概率.
(2)中国队与美国队比赛中,中国队获得积分X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出中国队获得积分X的分布列和数学期望EX.
解答 解:(1)∵根据以往数据统计分析,中国队与美国队的每局比赛中,中国队获胜的概率为$\frac{2}{3}$,
∴在中国队先输一局的情况下,中国队本场比赛获胜的概率:
p=$(\frac{2}{3})^{3}$+${C}_{3}^{2}(\frac{2}{3})^{2}(\frac{1}{3})(\frac{2}{3})$=$\frac{16}{27}$.
(2)中国队与美国队比赛中,中国队获得积分X的可能取值为0,1,2,3,
P(X=0)=$(\frac{1}{3})^{3}+{C}_{3}^{1}(\frac{2}{3})(\frac{1}{3})^{2}(\frac{1}{3})$=$\frac{1}{9}$,
P(X=1)=${C}_{4}^{2}(\frac{2}{3})^{2}(\frac{1}{3})^{2}(\frac{1}{3})$=$\frac{8}{81}$,
P(X=2)=${C}_{4}^{2}(\frac{2}{3})^{2}(\frac{1}{3})^{2}(\frac{2}{3})$=$\frac{16}{81}$,
P(X=3)=$(\frac{2}{3})^{3}+{C}_{3}^{2}(\frac{2}{3})^{2}(\frac{1}{3})$($\frac{2}{3}$)=$\frac{16}{27}$,
∴中国队获得积分X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{9}$ | $\frac{8}{81}$ | $\frac{16}{81}$ | $\frac{16}{27}$ |
点评 本题考查概率的求法,考查中国队获得积分的分布列和数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a0<1,函数f(x)=xa0(x>0)是减函数 | B. | ?a>1,函数f(x)=xa(x>0)不是减函数 | ||
| C. | ?a0>1,函数f(x)=xa(x>0)不是增函数 | D. | ?a>1,函数f(x)=xa(x>0)是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$π | B. | $\frac{1}{2}$π | C. | $\frac{3}{4}$π | D. | $\frac{3}{8}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
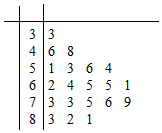 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com