
分析 ( I)设数列{an}的公比为q,从而由a${\;}_{3}^{2}$=2a2a5及a1+2a2=1可解得q=$\frac{1}{2}$,a1=$\frac{1}{2}$,从而解得;
( II)化简bn=log2a1+log2a2+…+log2an=-(1+2+3+…+n)=-$\frac{n(n+1)}{2}$,故$\frac{1}{{b}_{n}}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$),从而求和.
解答 解:( I)设数列{an}的公比为q,
由a${\;}_{3}^{2}$=2a2a5得(a1q2)2=2a1q•a1•q4,
∴q=$\frac{1}{2}$,
由a1+2a2=1得a1=$\frac{1}{2}$.
故数列{an}的通项公式为an=$\frac{1}{{2}^{n}}$.
( II)bn=log2a1+log2a2+…+log2an=-(1+2+3+…+n)=-$\frac{n(n+1)}{2}$,
∴$\frac{1}{{b}_{n}}$=-$\frac{2}{n(n+1)}$=-2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Sn=-2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)]=-$\frac{2n}{n+1}$.
点评 本题考查了等比数列的性质的应用及对数运算的应用,同时考查了裂项求和法应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | |z1|<|z2| | B. | |z1|=|z2| | C. | |z1|>|z2| | D. | 无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
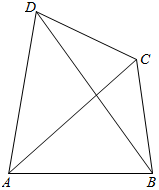 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 210.5 | C. | 211.5 | D. | 212.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{10}$ | D. | $\frac{\sqrt{173}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 26 | C. | 25 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com