
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
分析 (1)记事件A“该公司在星期一至少有2辆车出车”,利用独立重复试验的概率的乘法,转化求解即可.
(2)X的可能取值为0,1,2,3,4,5,求出概率,得到分布列,然后求解期望即可.
解答 (本小题满分12分)
解:(1)记事件A“该公司在星期一至少有2辆车出车”,
则$p(A)=1-{(\frac{1}{2})^3}{(\frac{1}{3})^2}-C_3^1{(\frac{1}{2})^3}{(\frac{1}{3})^2}-C_2^1{(\frac{1}{2})^3}(\frac{1}{3})(\frac{2}{3})$…(2分)
=$1-\frac{1}{72}-\frac{3}{72}-\frac{4}{72}$(3分)
=$\frac{8}{9}$…(4分)
(2)X的可能取值为0,1,2,3,4,5,
$P({X=0})={({\frac{1}{3}})^2}•{({\frac{1}{2}})^3}=\frac{1}{72}$;$P({X=1})=C_2^1•\frac{2}{3}•\frac{1}{3}•{({\frac{1}{2}})^3}$$+{({\frac{1}{3}})^2}•C_3^1•{({\frac{1}{2}})^3}=\frac{7}{72}$;$P({X=2})={({\frac{2}{3}})^2}•{({\frac{1}{2}})^3}+C_2^1•\frac{2}{3}•\frac{1}{3}•C_3^1{({\frac{1}{2}})^3}$$+{({\frac{1}{3}})^2}•C_3^2•{({\frac{1}{2}})^3}=\frac{19}{72}$;
$P({X=3})={({\frac{2}{3}})^2}•C_3^1•{({\frac{1}{2}})^3}$$+C_2^1•\frac{2}{3}•\frac{1}{3}•C_3^2•{({\frac{1}{2}})^3}+{({\frac{1}{3}})^2}•{({\frac{1}{2}})^3}=\frac{25}{72}$;$P({X=4})={({\frac{2}{3}})^2}•C_3^2•{({\frac{1}{2}})^3}+C_2^1•\frac{2}{3}•\frac{1}{3}•{({\frac{1}{2}})^3}=\frac{16}{72}$;$P({X=5})={({\frac{2}{3}})^2}•{({\frac{1}{2}})^3}=\frac{4}{72}$;…(10分)
∴X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{72}$ | $\frac{7}{72}$ | $\frac{19}{72}$ | $\frac{25}{72}$ | $\frac{16}{72}$ | $\frac{4}{72}$ |
点评 本题考查独立重复试验的概率的求法,分布列以及期望的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
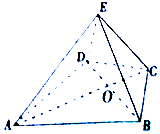 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com