
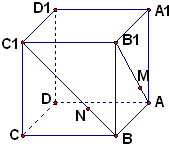
 在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:
在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:分析 由题意在四条棱A1A,B1B,C1C,D1D上分别取点G,F,E,H四点,使AG=$\frac{1}{3}$A1A,BF=$\frac{1}{3}$B1B,CE=$\frac{1}{3}$C1C,DH=$\frac{1}{3}$D1D,得到平面GFEH,则点M,N在与平面A1B1C1D1平行的平面GFEH中.利用线面垂直的性质判断①正确;利用平行公理判断②错误;利用面面平行的性质判断③正确;利用面面平行以及线线垂直的性质判断④错误.
解答 解;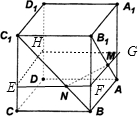 在正方体ABCD-A1B1C1D1的四条棱A1A,B1B,C1C,D1D上分别取点G,F,E,H四点,
在正方体ABCD-A1B1C1D1的四条棱A1A,B1B,C1C,D1D上分别取点G,F,E,H四点,
使AG=$\frac{1}{3}$A1A,BF=$\frac{1}{3}$B1B,CE=$\frac{1}{3}$C1C,DH=$\frac{1}{3}$D1D,连接GF,FE,EH,HG,
∵点M、N分别在AB1、BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,
∴M在线段GF上,N点在线段FE上.且四边形GFEH为正方形,平面GFEH∥平面A1B1C1D1,
∵AA1⊥平面A1B1C1D1,∴AA1⊥平面GFEH,
∵MN?平面GFEH,∴AA1⊥MN,故①正确;
∵A1C1∥GE,而GE与MN不平行,∴A1C1与MN不平行,故②错误;
∵平面GFEH∥平面A1B1C1D1,MN?平面GFEH,∴MN∥平面A1B1C1D1,故③正确;
∵B1D1∥FH,FH?平面GFEH,MN?平面GFEH,且MN与FH不垂直,∴B1D1与MN不垂直,故④错误.
∴正确命题只有①③.
故答案为:①③.
点评 本题主要考查立体几何中,线线,线面,面面平行与垂直性质的应用,考查了学生推论能力和空间想象力,属中档题.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
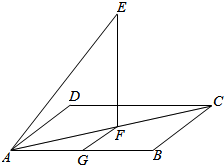 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题:
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com