
分析 (1)利用导数先研究函数的单调性,然后根据单调性求出函数的最值;
(2)先对函数H2(x)求导数,然后研究该函数在(0,+∞)上的单调性,求其最大值,用b表示,该最大值满足小于零即可,解不等式组获得b的范围;
(3)结合(2)的结论可先构造函数,然后利用函数的单调性构造不等式,使问题获得证明.注意在化简求和时的方法.
解答 解:(1)函数H(x)的定义域为(-1,+∞),
又${H}_{1}′(x)=\frac{1}{(1+x)^{2}}-\frac{1}{1+x}=\frac{-x}{(1+x)^{2}}$,令H1′(x)=0得x=0.
当x∈(-1,0)时,H1′(x)>0,H1(x)递增;当x∈(0,+∞)时,H1′(x)<0,H1(x)递减.
所以函数H1(x)的最大值为H1(0)=0.
(2)由已知得:${H}_{2}′(x)=\frac{1}{1+x}-b$,
①若b≥1,则x∈[0,+∞)时,H2′(x)≤0,所以H2(x)=g(x)-bx在[0,+∞)上为减函数,
所以H2(x)=ln(1+x)-bx<H2(0)=0在[0,+∞)恒成立.
②若b≤0,则x∈[0,+∞)时,${H}_{2}′(x)=\frac{1}{1+x}-b>0$,所以H2(x)=g(x)-bx在[0,+∞)上为增函数,
所以H2(x)=ln(1+x)-bx>H(0)=0,不能使H2(x)<0在[0,+∞)上恒成立.
③若0<b<1,则由H′2(x)=0得x=$\frac{1}{b}-1$,
当x∈[$0,\frac{1}{b}-1$)时,H2′(x)>0,所以H2(x)在[0,$\frac{1}{b}-1$)上为增函数,
所以H2(x)=ln(1+x)-bx>H2(0)=0,所以不能使H2(x)<0在[0,+∞)上恒成立.
综上所述,b的取值范围是[1,+∞).
(3)由以上得:$\frac{x}{1+x}<ln(1+x)<x(x>0)$.
取x=$\frac{1}{n}$得:$\frac{1}{1+n}<ln(1+\frac{1}{n})<\frac{1}{n}$.
令${x}_{n}=\sum_{k=1}^{n}\frac{k}{{k}^{2}+1}-lnn$,则${x}_{1}=\frac{1}{2}$,
当n≥2时,${x}_{n}-{x}_{n-1}=\frac{n}{{n}^{2}+1}-ln(1+\frac{1}{n-1})$$<\frac{n}{{n}^{2}+1}-\frac{1}{n}$=-$\frac{1}{({n}^{2}+1)n}<0$.
因此${x}_{n}<{x}_{n-1}<…{x}_{1}=\frac{1}{2}$,即$\sum_{k=1}^{n}\frac{k}{{k}^{2}+1}-lnn≤\frac{1}{2}$.
又lnn=$\sum_{k=2}^{n}[lnk-ln(k-1)]+ln1=\sum_{k=1}^{n-1}ln(1+\frac{1}{k})$,
故xn=$\sum_{i=1}^{n}$$\frac{k}{{k}^{2}+1}$-$\sum_{i=1}^{n-1}$ln(1+$\frac{1}{k}$)
=$\sum_{k=1}^{n-1}[\frac{k}{{k}^{2}+1}-ln(1+\frac{1}{k})]+\frac{n}{{n}^{2}+1}$$>\sum_{k=1}^{n-1}(\frac{k}{{k}^{2}+1}-\frac{1}{k})=-\sum_{k=1}^{n-1}\frac{1}{({k}^{2}+1)k}$
>$-\sum_{k=1}^{n-1}\frac{1}{(k+1)k}$=-1+$\frac{1}{n}>-1$.
综上所述,不等式-1<$\sum_{k=1}^n{\frac{k}{{{k^2}+1}}}$-lnn≤$\frac{1}{2}$(n=1,2,…)成立.
点评 本题考查了利用函数的单调性研究函数的最值问题,以及不等式恒成立问题的解题思路,同时第三问还涉及到放缩法的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. | 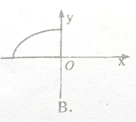 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示茎叶图记录了甲、乙两组各5名同学参加社会实践活动的次数.
如图所示茎叶图记录了甲、乙两组各5名同学参加社会实践活动的次数.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2π,2016π) | B. | ($\frac{3π}{2},\frac{4031π}{2}$) | C. | (2π,2015π) | D. | (π,2015π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com