Question

设点P，M，N分别在函数y=2x+2，y=

4x-x2

，y=x+3的图象上，且

MN

=2

PN

，则点P横坐标的取值范围为

 

．

Answer 1

考点：向量数乘的运算及其几何意义

专题：平面向量及应用

分析：如图所示，由

MN

=2

PN

，可得点P是线段MN的中点．设M（x₁，y₁），P（x，y），N（x₂，y₂）．可得x=

x1+x2

2

，y=

y1+y2

2

，y1=

4x1- x 2 1

，（0≤x₁≤4），y₂=x₂+3，y=2x+2．化为2x=

4x1- x 2 1

-1-x₁（0≤x₁≤4）．
令f（t）=

4t-t2

-1-t（0≤t≤4）．利用导数研究其单调性极值与最值，即可得出．

解答： 解：如图所示，
∵

MN

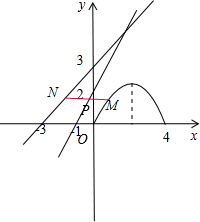
=2

PN

，
∴点P是线段MN的中点．
设M（x₁，y₁），P（x，y），N（x₂，y₂）．
∴x=

x1+x2

2

，y=

y1+y2

2

，y1=

4x1- x 2 1

，（0≤x₁≤4），
y₂=x₂+3，y=2x+2．
化为2x=

4x1- x 2 1

-1-x₁（0≤x₁≤4）．
令f（t）=

4t-t2

-1-t（0≤t≤4）．
f′（t）=

2-t

4t-t2

-1，
当2≤t≤4时，f′（t）＜0，函数f（t）单调递减．
当0≤t＜2时，f′（t）=0，解得t=2±

2

，则当0≤t＜2-

2

时，函数f（t）单调递增；
当2-

2

＜t＜2时，函数f（t）单调递减．
而极大值即最大值f(2-

2

)=2

2

-3，又f（0）=-1，f（4）=-5．
∴点P横坐标的取值范围为[-

5

2

，

2 2 -3

2

]．
故答案为：[-

5

2

，

2 2 -3

2

]．

点评：本题考查了利用导数研究函数的单调性极值与最值、向量的共线、分类讨论思想方法，考查了推理能力和计算能力，属于难题．