
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由87°=60°+27°,然后展开两角和的正弦,化简后与分母约分得答案.
解答 解:$\frac{sin87°-cos63°cos60°}{cos27°}$
=$\frac{sin(60°+27°)-\frac{1}{2}sin27°}{cos27°}$
=$\frac{sin60°cos27°+cos60°sin27°-\frac{1}{2}sin27°}{cos27°}$
=$\frac{\frac{\sqrt{3}}{2}cos27°+\frac{1}{2}sin27°-\frac{1}{2}sin27°}{cos27°}$
=$\frac{\frac{\sqrt{3}}{2}cos27°}{cos27°}=\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题考查三角函数的化简求值,考查了两角和的正弦,是基础题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
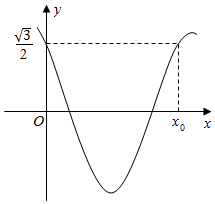 已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=2cosπx•cos2$\frac{φ}{2}$+sin[(x+1)π]•sinφ-cosπx(0<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|0<x<2} | D. | {x|x≤1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com