
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①利用否命题的定义,不等式的性质即可得出.
②依题意,利用复合命题的真值表可知p假q真,可判断②.
③由全称性命题的否定为存在性命题,即可判断③.
④分别讨论能否由x>1推出x2+x-2>0,能否由x2+x-2>0推出x>1,即可得到正确答案.
解答 解:对于①,命题“若x2>1,则x>1”,的否命题是“若x2≤1,则x≤1,”故①错误.
对于②:若命题“¬p”与命题“p或q”都是真命题,则p假q真,故②正确.
对于③:命题“?x∈R+,x-lnx>0”的否定是“?x0∈R+,x0-lnx0≤0”,则③正确.
对于④:当x>1时,x2+x-2>0成立,所以充分条件成立.
当x2+x-2>0时,x<-2或x>1,所以必要条件不成立.
故④错误.
故选:B.
点评 本题考查函数的单调性的运用,考查复合命题的真假和真值表的运用,考查充分必要条件的判断和命题的否定,属于基础题和易错题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα | B. | cosα | C. | sin$\frac{π}{3}$+cosα | D. | cos$\frac{π}{3}$+sinα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
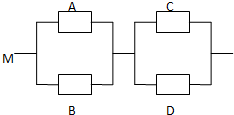 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | [3,4) | C. | (3,4) | D. | [3,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com