Question

6．设O为坐标原点，直线l：x-y+m=0与圆C：x²-2x+y²-7=0交于M，N两点，与x轴，y轴交于A，B两点，且$\sqrt{3}$|$\overrightarrow{MN}$|=3|$\overrightarrow{OM}$+$\overrightarrow{ON}$|，点P在直线l上，满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$，若$\overrightarrow{PO}$•$\overrightarrow{PC}$=3，则λ的值为4±$\sqrt{17}$或-3$±\sqrt{10}$．

Answer 1

分析 设M（x₁，y₁），N（x₂，y₂），联立直线方程和圆方程，运用韦达定理，以及向量的加法运算和模的公式，以及弦长公式，可得m的方程，解方程可得m的值，分别讨论m的值，设出P的坐标，求得A，B，C的坐标，运用向量的坐标运算和数量积的坐标表示，解方程即可得到所求值．

解答 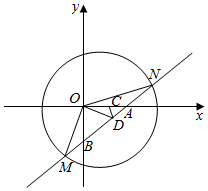解：设M（x₁，y₁），N（x₂，y₂），
由$\left\{\begin{array}{l}{x-y+m=0}\\{{x}^{2}-2x+{y}^{2}-7=0}\end{array}\right.$得2x²+（2m-2）x+m²-7=0，
∴x₁+x₂=1-m，y₁+y₂=1+m，
$\overrightarrow{OM}+\overrightarrow{ON}=（1-m，1+m）$，则|$\overrightarrow{OM}$+$\overrightarrow{ON}$|=$\sqrt{2+2{m}^{2}}$，
圆心C到MN的距离d²=$\frac{（1+m）^{2}}{2}$，
|$\overrightarrow{MN}$|²=4（r²-d²）=4（8-d²），
由|$\overrightarrow{MN}$|²=3|$\overrightarrow{OM}$+$\overrightarrow{ON}$|²得3m²+2d²=13，
⇒2m²+m-6=0，解得m=-2或m=$\frac{3}{2}$，
当m=-2时，设P（x，x-2），A（2，0），B（0，-2），C（1，0），
由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$，$\overrightarrow{PO}$•$\overrightarrow{PC}$=3，
可得（x-2，x-2）=λ（-x，-x），即有x-2=-λx，
（-x，2-x）•（1-x，2-x）=3，即有-x（1-x）+（2-x）²=3，
化为2x²-5x+1=0，
解得x=$\frac{5±\sqrt{17}}{4}$，λ=4±$\sqrt{17}$；
当m=$\frac{3}{2}$时，设P（x，x+$\frac{3}{2}$），A（-$\frac{3}{2}$，0），B（0，$\frac{3}{2}$），C（1，0），
由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$，$\overrightarrow{PO}$•$\overrightarrow{PC}$=3，
可得（x+$\frac{3}{2}$，x+$\frac{3}{2}$）=λ（-x，-x），即有x+$\frac{3}{2}$=-λx，
（-x，-$\frac{3}{2}$-x）•（1-x，-$\frac{3}{2}$-x）=3，即有-x（1-x）+（-$\frac{3}{2}$-x）²=3，
化为2x²+2x-$\frac{3}{4}$=0，
解得x=$\frac{-2±\sqrt{10}}{4}$，λ=-3$±\sqrt{10}$．
综上可得，λ=4±$\sqrt{17}$或λ=-3$±\sqrt{10}$．
故答案为：4±$\sqrt{17}$或-3$±\sqrt{10}$．

点评 本题考查直线和圆的位置关系，考查方程思想和向量的坐标运算和数量积的坐标表示，考查运算能力，属于中档题．