
【题目】以下四个关于圆锥曲线命题:
①“曲线![]() 为椭圆”的充分不必要条件是“
为椭圆”的充分不必要条件是“![]() ”;
”;
②若双曲线的离心率![]() ,且与椭圆
,且与椭圆![]() 有相同的焦点,则该双曲线的渐近线方程为
有相同的焦点,则该双曲线的渐近线方程为![]() ;
;
③抛物线![]() 的准线方程为
的准线方程为![]() ;
;
④长为6的线段![]() 的端点
的端点![]() 分别在
分别在![]() 、
、![]() 轴上移动,动点
轴上移动,动点![]() 满足
满足![]() ,则动点
,则动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
其中正确命题的序号为_________.
【答案】③④
【解析】
对于①, 求出“曲线![]() 为椭圆”的充要条件,判断与“
为椭圆”的充要条件,判断与“![]() ”关系,即得①的正误;对于②,根据已知条件求出双曲线的方程,从而求出渐近线方程,即得②的正误;对于③,把抛物线的方程化为标准式,求出准线方程,即得③的正误;对于④,设
”关系,即得①的正误;对于②,根据已知条件求出双曲线的方程,从而求出渐近线方程,即得②的正误;对于③,把抛物线的方程化为标准式,求出准线方程,即得③的正误;对于④,设![]() ,根据
,根据![]() ,可得
,可得![]() ,代入
,代入![]() ,求出动点
,求出动点![]() 的轨迹方程,即得④的正误.
的轨迹方程,即得④的正误.
对于①, “曲线![]() 为椭圆”的充要条件是“
为椭圆”的充要条件是“![]() 且
且![]() ”.
”.
所以“曲线![]() 为椭圆”的必要不充分条件是“
为椭圆”的必要不充分条件是“![]() ”,故①错误;
”,故①错误;
对于②,椭圆![]() 的焦点为
的焦点为![]() ,又双曲线的离心率
,又双曲线的离心率![]() ,所以双曲线的方程为
,所以双曲线的方程为![]() ,所以双曲线的渐近线方程为
,所以双曲线的渐近线方程为![]() ,故②错误;
,故②错误;
对于③,抛物线![]() 的方程化为标准式
的方程化为标准式![]() ,准线方程为
,准线方程为![]() ,故③正确;
,故③正确;
对于④,设![]() ,
,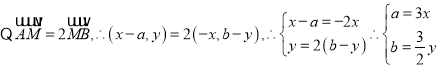 ,
,
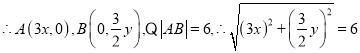 ,即
,即![]() ,即动点
,即动点![]() 的轨迹方程为
的轨迹方程为![]() .故④正确.
.故④正确.
故答案为:③④.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市有![]() ,
,![]() 两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,
两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,![]() 俱乐部每张球台每小时5元,
俱乐部每张球台每小时5元,![]() 俱乐部按月收费,一个月中
俱乐部按月收费,一个月中![]() 以内(含
以内(含![]() )每张球台90元,超过
)每张球台90元,超过![]() 的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于
的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于![]() ,也不超过
,也不超过![]() .
.
(1)设在![]() 俱乐部租一-张球台开展活动
俱乐部租一-张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,在
,在![]() 俱乐部租一张球台开展活动
俱乐部租一张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,试求
,试求![]() 和
和![]() 的解析式;
的解析式;
(2)问选择哪家俱乐部比较合算?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则方程
,则方程![]() 无实根”的否命题;
无实根”的否命题;
②命题“在![]() 中,
中,![]() ,那么
,那么![]() 为等边三角形”的逆命题;
为等边三角形”的逆命题;
③命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
④“若![]() ,则
,则![]() 的解集为
的解集为![]() ”的逆命题;
”的逆命题;
其中真命题的序号为( )
A.①②③④B.①②④C.②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,给定下列命题:
,给定下列命题:
①若方程![]() 有两个不同的实数根,则
有两个不同的实数根,则![]() ;
;
②若方程![]() 恰好只有一个实数根,则
恰好只有一个实数根,则![]() ;
;
③若![]() ,总有
,总有![]() 恒成立,则
恒成立,则![]() ;
;
④若函数![]() 有两个极值点,则实数
有两个极值点,则实数![]() .
.
则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科技改变生活,方便生活.共享单车的使用就是云服务的一种实践,它是指企业与政府合作,为居民出行提供单车共享服务,它符合低碳出行理念,为解决城市出行的“最后一公里”提供了有力支撑,是共享经济的一种新形态.某校学生社团为研究当地使用共享单车人群的年龄状况,随机抽取了当地![]() 名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
名使用共享单车的群众作出调查,所得频率分布直方图如图所示.
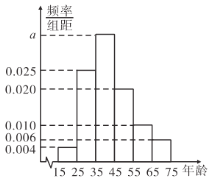
(1)估计当地共享单车使用者年龄的中位数;
(2)若按照分层抽样从年龄在![]() ,
,![]() 的人群中抽取
的人群中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人调查单车使用体验情况,记抽取的
人调查单车使用体验情况,记抽取的![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com