
分析 (1)先求导,再根据递推公式分别求出a2,a3,a4;
(2)利用数学归纳法证明即可,
(3)利用裂项求和和放缩法即可证明.
解答 解:(1)${f'_n}(x)={x^2}-(n+1)x+1$,a1=3,又${a_{n+1}}=a_n^2-(n+1){a_n}+1$,
∴${a_2}=a_1^2-2{a_1}+1=4$,${a_3}=a_2^2-2{a_2}+1=5$,${a_4}=a_3^2-2{a_3}+1=6$.
(2)猜想an=n+2,用数学归纳法证明.
当n=1时显然成立,
假设当n=k(k∈N*)时,ak=k+2,
则当n=k+1(k∈N*)时,
ak+1=ak2-(k+1)ak+1=(k+2)2-(k+1)(k+2)+1,
=k+3=(k+1)+2,
∴当n=k(k∈N*)时,猜想成立.
根据数学归纳法对一切n∈N*,an=n+2均成立.
(3)证明:当k≥2时,有$\frac{1}{{{{(2{a_k}-5)}^2}}}=\frac{1}{{{{(2k-1)}^2}}}$<$\frac{1}{(2k-1)(2k-3)}=\frac{1}{2}(\frac{1}{2k-3}-\frac{1}{2k-1})$,
∴n≥2时,有$\sum_{k=1}^n{\frac{1}{{{{(2{a_k}-5)}^2}}}}$<1+$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…($\frac{1}{2n-3}$-$\frac{1}{2n-1}$)]
=1+$\frac{1}{2}$(1-$\frac{1}{2n-1}$)<1+$\frac{1}{2}$=$\frac{3}{2}$.
又n=1时,$\frac{1}{{{{(2{a_k}-1)}^2}}}$=1<$\frac{3}{2}$.
故对一切n∈N*,有$\sum_{k=1}^n{\frac{1}{{{{(2{a_k}-5)}^2}}}}$<$\frac{3}{2}$.
点评 本题考查导数的运算法则,函数和数列的关系,数列递推式,考查数学归纳法的运用和裂项求和和放缩法的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
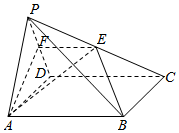 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0,1} | C. | {-1,1} | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com