
分析 由题意可知A在底面PBC的投影为底面正三角形的中心,设球半径为r,用r表示出由球心,△PBC的中心和P点构成的直角三角形的三边,使用勾股定理解出r,得出球的面积.
解答 解:∵BC=PB=PC=$\sqrt{2}$,AP=AB=AC=1,
∴三棱锥A-PBC为正三棱锥,
作AO⊥平面PBC,则O为正三角形PBC的中心,且PO=$\frac{\sqrt{6}}{3}$.
∴OA=$\sqrt{P{A}^{2}-O{P}^{2}}$=$\frac{\sqrt{3}}{3}$.
设外接球球心为M,半径为r,则PM=r,MO=|$\frac{\sqrt{3}}{3}$-r|,
由勾股定理得:r2=($\frac{\sqrt{6}}{3}$)2+($\frac{\sqrt{3}}{3}$-r)2,
解得r=$\frac{\sqrt{3}}{2}$.
∴球的表面积S=4πr2=3π.
故答案为:3π.
点评 本题考查了棱锥与外接球的关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 蒙特卡洛方法的思想如下:当所求解的问题是某种随机事件=出现的概率时,通过某种“试验”方法,以这种事件出现的频率估计这一随机事件的概率,并将其作为问题的解.现为了估计右图所示的阴影部分面积的大小,使用蒙特卡洛方法的思想,向面积为16的矩形OABC内投掷800个点,其中恰有180个点落在阴影部分内,则可估计阴影部分的面积为( )
蒙特卡洛方法的思想如下:当所求解的问题是某种随机事件=出现的概率时,通过某种“试验”方法,以这种事件出现的频率估计这一随机事件的概率,并将其作为问题的解.现为了估计右图所示的阴影部分面积的大小,使用蒙特卡洛方法的思想,向面积为16的矩形OABC内投掷800个点,其中恰有180个点落在阴影部分内,则可估计阴影部分的面积为( )| A. | 3.6 | B. | 4 | C. | 12.4 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+{y^2}$=1 | B. | $\frac{y^2}{4}+{x^2}$=1 | ||
| C. | $\frac{x^2}{4}+{y^2}$=1或$\frac{y^2}{4}+{x^2}$=1 | D. | $\frac{y^2}{4}+\frac{x^2}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
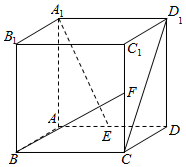 如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.
如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{7}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x)是周期函数,且周期T=3 | B. | 函数y=f(x)在R上有可能是单调函数 | ||
| C. | 函数y=f(x)的图象关于点$(-\frac{3}{4},0)$对称 | D. | 函数y=f(x)是R上的偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com