Question

1．已知ABCDEF是正六边形，在下列4个表达式
（1）$\overrightarrow{FE}$+$\overrightarrow{ED}$，（2）2$\overrightarrow{BC}$+$\overrightarrow{DC}$，（3）$\overrightarrow{BC}$+$\overrightarrow{CD}$+$\overrightarrow{EC}$，（4）2$\overrightarrow{ED}$-$\overrightarrow{FA}$中，运算结果与$\overrightarrow{AC}$相等的表达式共有4个．

Answer 1

分析 根据平面向量的加减运算法则，结合图形，进行化简，即可得出正确的结论．

解答 解：（1）如图1所示，正六边形ABCDEF中，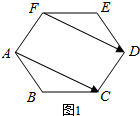
$\overrightarrow{FE}$+$\overrightarrow{ED}$=$\overrightarrow{FD}$=$\overrightarrow{AC}$，
（2）如图2所示，
2$\overrightarrow{BC}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$=$\overrightarrow{AC}$，
（3）如图3所示，
$\overrightarrow{BC}$+$\overrightarrow{CD}$+$\overrightarrow{EC}$=$\overrightarrow{BD}$+$\overrightarrow{FB}$=$\overrightarrow{FD}$=$\overrightarrow{AC}$，
（4）如图4所示，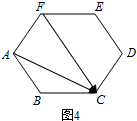
2$\overrightarrow{ED}$-$\overrightarrow{FA}$=$\overrightarrow{FC}$-$\overrightarrow{FA}$=$\overrightarrow{AC}$，
综上，运算结果与$\overrightarrow{AC}$相等的表达式有4个．
故答案为：4．

点评 本题考查了平面向量的应用问题，解题时应画出图形，结合图形进行解答，是基础题目．