
|
A、
| ||
B、
| ||
C、
| ||
D、
|
|
 解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,
解:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤2,0≤c≤2所表示的区域表示出来,
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| N(A) |
| N |


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
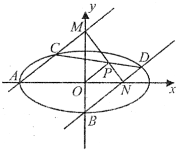 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.| AM |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、当k=2013时,f(x)在x=1处取得极小值 |
| B、当k=2013时,f(x)在x=1处取得极大值 |
| C、当k=2014时,f(x)在x=1处取得极小值 |
| D、当k=2014时,f(x)在x=1处取得极大值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com