
���� ��1���������й���a��b��c�ķ����飬��ⷽ����ɵ�a��b��c��ֵ������Բ���̿���
��2����ֱ��AB�ķ���Ϊx=ty+m��t��R����A��x1��y1����B��x2��y2��������x1��x2����AB���е�ΪM������ֱ��ϵ���̺���Բ���̣���Ϊ����y��һԪ���η��̣���AB��ֱ��x���AB����ֱx�����ۣ���AB��ֱ��x��ʱ��ֱ�����Q������ꣻ��AB����ֱx��ʱ���ɡ�ABQΪ�ȱ������Σ���m������⣮
��� �⣺��1���������$\left\{\begin{array}{l}{\frac{2{b}^{2}}{a}=1}\\{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=\sqrt{3}}\end{array}\right.$��
���������Բ����Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��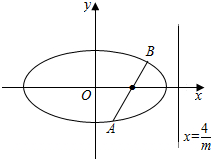
��2����ֱ��AB�ķ���Ϊx=ty+m��t��R����
A��x1��y1����B��x2��y2��������x1��x2��
��AB���е�ΪM����$\left\{\begin{array}{l}{x=ty+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$���ã�4+t2��y2+2tmy+m2-4=0��
���=4t2m2-4��4+t2����m2-4��=16��t2+4-m2����0��
${y}_{1}+{y}_{2}=-\frac{2tm}{4+{t}^{2}}$��${y}_{1}{y}_{2}=\frac{{m}^{2}-4}{4+{t}^{2}}$��
|y1-y2|=$\sqrt{��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{��-\frac{2tm}{4+{t}^{2}}��^{2}-4\frac{{m}^{2}-4}{4+{t}^{2}}}$=$\frac{4\sqrt{{t}^{2}+4-{m}^{2}}}{4+{t}^{2}}$��
${x}_{1}+{x}_{2}=t��{y}_{1}+{y}_{2}��+2m=\frac{8m}{4+{t}^{2}}$��
���M�����${x}_{M}=\frac{{x}_{1}+{x}_{2}}{2}=\frac{4m}{4+{t}^{2}}$��������${y}_{M}=\frac{{y}_{1}+{y}_{2}}{2}=-\frac{tm}{4+{t}^{2}}$��
������ֱ��l�ϴ��ڵ�Q��ʹ�á�ABQΪ�ȱ������Σ�
�ǵ�Q������Ϊ��$\frac{4}{m}��n$��������QM����QM��AB��
�ٵ�ֱ��AB��ֱ��x��ʱ��A��m��$-\frac{\sqrt{4-{m}^{2}}}{2}$����B��m��$\frac{\sqrt{4-{m}^{2}}}{2}$����
��Q������ֻ���ǣ�$\frac{4}{m}��0$����
|AB|=$\sqrt{4-{m}^{2}}$��|QM|=$\frac{4}{m}-m$��
����ABQΪ�ȱ������Σ���$\frac{\sqrt{4-{m}^{2}}}{\frac{4}{m}-m}=\frac{2}{\sqrt{3}}$�����${m}^{2}=\frac{16}{7}��4$��
����ʱ��ֱ��l�ϴ��ڵ�Q��$\sqrt{7}$��0����ʹ�á�ABQΪ�ȱ������Σ�
�ڵ�ֱ��AB����ֱ��x��ʱ��${k}_{QM}=\frac{mn��4+{t}^{2}��+t{m}^{2}}{4��4+{t}^{2}��-4{m}^{2}}$��${k}_{AB}=\frac{1}{t}$��
${k}_{QM}•{k}_{AB}=\frac{mn��4+{t}^{2}��+t{m}^{2}}{4��4+{t}^{2}��}•\frac{1}{t}=-1$����n=$\frac{3tm}{4+{t}^{2}}-\frac{4t}{m}$��
|QM|=$\frac{4\sqrt{{t}^{2}+1}��4+{t}^{2}-{m}^{2}��}{��4+{t}^{2}��m}$��|AB|=$\sqrt{1+{t}^{2}}|{y}_{1}-{y}_{2}|=\sqrt{1+{t}^{2}}\frac{4\sqrt{4+{t}^{2}-{m}^{2}}}{4+{t}^{2}}$��
����ABQΪ�ȱ������Σ���$\frac{|QM|}{|AB|}=\frac{\sqrt{3}}{2}$����${t}^{2}=\frac{7{m}^{2}}{4}-4$��n=$\frac{3tm}{4+{t}^{2}}-\frac{4t}{m}=t��\frac{3m}{4+{t}^{2}}-\frac{4}{m}��=-\frac{16t}{7m}$��
��0��m��$\frac{4\sqrt{7}}{7}$ʱ��t�����ڣ�
��$\frac{4\sqrt{7}}{7}$��m��2ʱ��t=$\sqrt{\frac{7{m}^{2}}{4}-4}$ʱ��n=-$\frac{8\sqrt{7{m}^{2}-16}}{7m}$��
t=-$\sqrt{\frac{7{m}^{2}}{4}-4}$ʱ��n=$\frac{8\sqrt{7{m}^{2}-16}}{7m}$��
���ϣ���0��m��$\frac{4\sqrt{7}}{7}$ʱ��ֱ��l�ϲ����ڵ�Q��ʹ�á�ABQΪ�ȱ������Σ�
��m=$\frac{4\sqrt{7}}{7}$ʱ��ֱ��l�ϴ���һ����Q��ʹ�á�ABQΪ�ȱ������Σ�Q��$\sqrt{7}$��0����
��$\frac{4\sqrt{7}}{7}$��m��2��t=$\sqrt{\frac{7{m}^{2}}{4}-4}$ʱ����ֱ��l�����ҽ���һ����Q��$\frac{4}{m}$��-$\frac{8\sqrt{7{m}^{2}-16}}{7m}$����ʹ�á�ABQΪ�ȱ������Σ�
��$\frac{4\sqrt{7}}{7}$��m��2��t=-$\sqrt{\frac{7{m}^{2}}{4}-4}$ʱ����ֱ��l�����ҽ���һ����Q��$\frac{4}{m}$��$\frac{8\sqrt{7{m}^{2}-16}}{7m}$����ʹ�á�ABQΪ�ȱ������Σ�
���� ���⿼����Բ���̡�ֱ������Բ��λ�ù�ϵ������ת���뻯��˼�롢���ν��˼�롢�����뷽��˼�뼰���������������������2���Ĺؼ��ǰ�ͼ��ת��Ϊ���ʵ�λ�ù�ϵ��������ϵ������ת��Ϊ����������⣬��ͨ�������ֶ����������ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
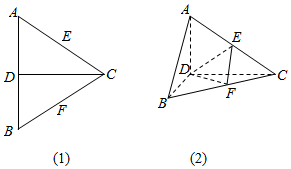 ��ͼ��1������������ABC�߳�Ϊ2a��CD��AB���ϵĸߣ�E��F�ֱ�ΪAC��BC���ϵ��е㣬�ֽ���ABC��CD���۳�ֱ�����A-DC-B����ͼ��2����
��ͼ��1������������ABC�߳�Ϊ2a��CD��AB���ϵĸߣ�E��F�ֱ�ΪAC��BC���ϵ��е㣬�ֽ���ABC��CD���۳�ֱ�����A-DC-B����ͼ��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
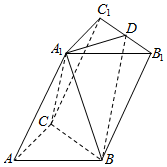 ��ͼ����������ABC-A1B1C1�У���BAC=90�㣬AB=AC=2��AA1=4��A1�ڵ���ABC����ӰΪBC���е�E��D��B1C1���е㣮
��ͼ����������ABC-A1B1C1�У���BAC=90�㣬AB=AC=2��AA1=4��A1�ڵ���ABC����ӰΪBC���е�E��D��B1C1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
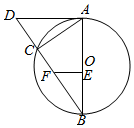 ��ͼ��O��Rt��ABC�����Բ��E��F��AB��BC�ϵĵ㣬��A��E��F��C�ĵ㹲Բ���ӳ�BC��D��ʹ��AC•BF=AD•BE��
��ͼ��O��Rt��ABC�����Բ��E��F��AB��BC�ϵĵ㣬��A��E��F��C�ĵ㹲Բ���ӳ�BC��D��ʹ��AC•BF=AD•BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
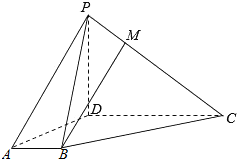 ��ͼ������P-ABCD�У�PD�͵���ABCD��AB��CD����BAD=$\frac{��}{3}$��AB=1��CD=3��MΪPC��һ�㣬MC=2PM��
��ͼ������P-ABCD�У�PD�͵���ABCD��AB��CD����BAD=$\frac{��}{3}$��AB=1��CD=3��MΪPC��һ�㣬MC=2PM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com