
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的零点的个数;
的零点的个数;
(2)当函数![]() 有两个零点时,证明:
有两个零点时,证明:![]() .
.
【答案】(1)见解析;(2)证明见解析
【解析】
(1)分别讨论![]() ,
,![]() ,
,![]() 时
时![]() 的单调性,进而判断零点个数;
的单调性,进而判断零点个数;
(2)由(1)可知![]() 时
时![]() 有两个零点,
有两个零点, ![]() ,设
,设![]() ,由
,由![]() ,
,![]() 可得存在
可得存在![]() ,则
,则![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,即
上是增函数,即![]() 为最小值,故证明
为最小值,故证明![]() 即可.
即可.
(1)由题,![]()
当![]() 时,
时,![]() 在
在![]() 上是增函数
上是增函数
又![]() 时
时![]() ,
,![]()
∴![]() 有一个零点
有一个零点
当![]() 时
时![]() ,∴
,∴![]() 无零点
无零点
当![]() 时
时![]() 在
在![]() 上是增函数
上是增函数
又![]() 时
时![]() ,
,![]() 时
时![]() ,
,
∴![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]()
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数
又![]() 时
时![]() ,
,![]() 时
时![]() ,
,
当![]() 时,
时,![]()
∴![]() 有两个零点
有两个零点
当![]() 时,
时,![]() ,∴
,∴![]()
∴![]()
∴![]() 有一个零点
有一个零点
当![]() 时,
时,
当![]() 时
时![]() ,
,![]() 在
在![]() 上无零点
上无零点
当![]() 时
时![]()
∴![]()
∴![]() 在
在![]() 上也无零点
上也无零点
∴![]() 在
在![]() 上无零点
上无零点
综上:![]() 时
时![]() 有两个零点
有两个零点
![]() 或
或![]() 时
时![]() 有一个零点
有一个零点
![]() 时
时![]() 无零点
无零点
(2)证明:由(1)知![]() ,
,![]()
![]()
令![]() ,
,![]() 在
在![]() 上是增函数
上是增函数
又![]() ,
,![]()
∴存在![]() ,使
,使![]()
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数
∴![]()
∵![]()
∴![]()
∴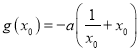
∵![]()
∴![]()
又![]()
∴![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
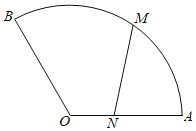
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查者中恰有1名对手机游戏无兴趣的概率.
附: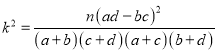
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
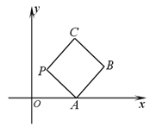
【题目】如图所示,在平面直角坐标系![]() 上放置一个边长为1的正方形
上放置一个边长为1的正方形![]() ,此正方形
,此正方形![]() 沿
沿![]() 轴滚动(向左或向右均可),滚动开始时,点
轴滚动(向左或向右均可),滚动开始时,点![]() 位于原点处,设顶点
位于原点处,设顶点![]() 的纵坐标与横坐标的函数关系式
的纵坐标与横坐标的函数关系式![]() ,
,![]() ,该函数相邻两个零点之间的距离为
,该函数相邻两个零点之间的距离为![]() .
.
(1)写出![]() 的值并求出顶点
的值并求出顶点![]() 到
到![]() 的最小运动路径的长度
的最小运动路径的长度![]() 的值;
的值;
(2)写出函数![]() ,
,![]() ,
,![]() 的表达式;并研究该函数除周期外的基本性质(无需证明).
的表达式;并研究该函数除周期外的基本性质(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中无理数
,其中无理数![]() .
.
(Ⅰ)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的极值点有三个,最小的记为
的极值点有三个,最小的记为![]() ,最大的记为
,最大的记为![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:①在回归分析中,可用相关系数r的值判断模型的拟合效果,|r|越大,模拟的拟合效果越好;②在一组样本数据![]() 不全相等)的散点图中,若所有样本点
不全相等)的散点图中,若所有样本点![]() 都在直线
都在直线![]() 上,则这组样本数据的线性相关系数为
上,则这组样本数据的线性相关系数为![]() ;③对分类变量x与y的随机变量
;③对分类变量x与y的随机变量![]() 来说,
来说,![]() 越小,判断“x与y有关系”的把握程度越大.其中真命题的个数为__________.
越小,判断“x与y有关系”的把握程度越大.其中真命题的个数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com