
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$或$2\sqrt{2}$ | D. | 2 |
分析 设A位于第一象限,根据双曲线的渐近线方程,即可求得A点坐标,根据四边形的面积公式,即可求得a的值.
解答 解:根据对称性,不妨设A在第一象限,A(x,y),双曲线的渐近线方程y=±$\frac{2\sqrt{3}}{a}$x,
由题意可知:$\left\{\begin{array}{l}{y=\frac{2\sqrt{3}}{a}x}\\{{x}^{2}+{y}^{2}={a}^{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{{a}^{2}}{\sqrt{{a}^{2}+12}}}\\{y=\frac{2\sqrt{3}a}{\sqrt{{a}^{2}+12}}}\end{array}\right.$,
由四边形的ABCD的面积为S=4xy=$2\sqrt{3}a$,
则4×$\frac{{a}^{2}}{\sqrt{{a}^{2}+12}}$×$\frac{2\sqrt{3}a}{\sqrt{{a}^{2}+12}}$=$2\sqrt{3}a$,
解得:a=2,
∴a的值为2,
故选D.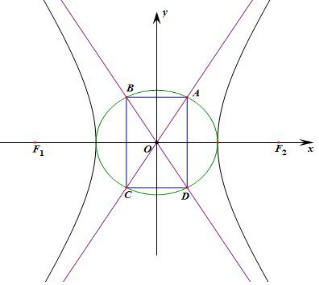
点评 本题考查双曲线的简单几何性质,双曲线的渐近线方程,考查计算能力,属于中档题.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a | B. | b | C. | $\sqrt{ab}$ | D. | $\frac{a+b}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 除夕18时PM2.5浓度 | 初一2时PM2.5浓度 | |
| 北京 | 75 | 647 |
| 天津 | 66 | 400 |
| 石家庄 | 89 | 375 |
| 廊坊 | 102 | 399 |
| 太原 | 46 | 115 |
| 上海 | 16 | 17 |
| 南京 | 35 | 44 |
| 杭州 | 131 | 39 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com