
| NP |
| NQ |
| GQ |
| NP |
| NP |
| NQ |
| GQ |
| NP |
| NP |
| NQ |
| GQ |
| NP |
| x2 |
| 4 |
| y2 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 某耐磨厂对一批耐磨球的单个重量(单位:克)进行了抽样检测,并绘制出频率分布直方图,已知耐磨球单个重量的范围为[96,106],样本数据分组为[96,98),[98,100),[100,104),[104,106)
某耐磨厂对一批耐磨球的单个重量(单位:克)进行了抽样检测,并绘制出频率分布直方图,已知耐磨球单个重量的范围为[96,106],样本数据分组为[96,98),[98,100),[100,104),[104,106)查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
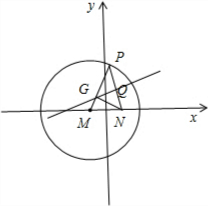
 如图,动圆D过定点A(0,2),圆心D在抛物线x2=4y上运动,MN为圆D在x轴上截得的弦,当圆心D运动时,记|AM|=m,|AN|=n.
如图,动圆D过定点A(0,2),圆心D在抛物线x2=4y上运动,MN为圆D在x轴上截得的弦,当圆心D运动时,记|AM|=m,|AN|=n.| m2+n2 |
| mn |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=
如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com