
分析 (1)⊙C:x2+y2+2x-4y+3=0,化为标准方程,求出圆心C,半径r.分类讨论,利用C到l的距离为1,即可求直线l的方程;
(2)设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得3x+4y-12=0,求|PM|的最小值,即求|PO|的最小值,即求原点O到直线2x-4y+3=0的距离.
解答 解:(1)x2+y2+2x-4y+3=0可化为(x+1)2+(y-2)2=2.
当l的斜率不存在时,其方程为x=-2,与圆C的交点为A(-2,1),B(-2,3)
|AB|=2,符合题意;
当l的斜率存在时,设其方程为y=k(x+2)即kx-y+2k=0
则C到l的距离d=$\frac{|-k-2+2k|}{\sqrt{{k}^{2}+1}}$=1
解得k=$\frac{3}{4}$,
∴l的方程为3x-4y+6=0
综上,直线l的方程为x=-2或3x-4y+6=0.
(2)如图:PM为圆C的切线,则CM⊥PM,∴△PMC为直角三角形,
∴|PM|2=|PC|2-|MC|2.
设P(x,y),C(-1,2),|MC|=$\sqrt{2}$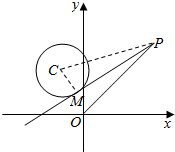
∵|PM|=|PO|,
∴x2+y2=(x+1)2+(y-2)2-2.
化简得点P的轨迹方程为2x-4y+3=0.
求|PM|的最小值,即求|PO|的最小值,即求原点O到直线2x-4y+3=0的距离,
代入点到直线的距离公式可求得|PM|最小值为$\frac{3\sqrt{5}}{10}$.
点评 本题考查直线方程,考查直线与圆的位置关系,考查了圆的切线的性质、勾股定理、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±512 | B. | 512 | C. | ±1024 | D. | 1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|0≤x≤2} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
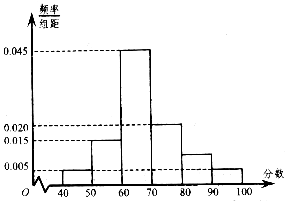 上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.
上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:5 | B. | 9:25 | C. | 5:$\sqrt{41}$ | D. | 7:9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com