
(本小题满分12分)已知函数 .
.
(Ⅰ)设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅱ)若对任意 恒有
恒有 ,求
,求 的取值范围.
的取值范围.
解:(1) 解析
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
(本小题满分14分)设函数
科目:高中数学
来源:
题型:解答题
已知定义在R上的函数
科目:高中数学
来源:
题型:解答题
(本小题满分10分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 的定义域为(
的定义域为( ,1)
,1) (1,
(1, )
)

因为 (其中
(其中 )恒成立,所以
)恒成立,所以 .…………………2分
.…………………2分
当 时,
时, 在(
在( ,0)
,0) (1,
(1, )上恒成立,所以
)上恒成立,所以 在(
在( ,1)
,1) (1,
(1, )上为增函数; …………………………………4分
)上为增函数; …………………………………4分
当 时,
时, 在(
在( ,0)
,0) (0,1)
(0,1) (1,
(1, )上恒成立,所以
)上恒成立,所以 在(
在( ,1)
,1) (1,
(1, )上为增函数;……………………………
)上为增函数;…………………………… ……6分
……6分
当 时,
时, 的解为:(
的解为:( ,
,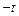 )
) (t,1)
(t,1) (1,+
(1,+ )
)
(其中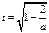 ).
).
所以 在各区间内的增减性如下表:
在各区间内的增减性如下表:区间 (  ,
,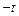 )
)( 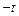 ,t)
,t)(t,1) (1,+  )
) 的符号
的符号+ 
+ +  的单调性
的单调性增函数


寒假作业江西高校出版社系列答案
寒假作业欢乐共享快乐假期系列答案
寒假作业及活动系列答案
寒假作业浙江教育出版社系列答案
寒假作业延边教育出版社系列答案
寒假作业团结出版社系列答案
寒假作业江西人民出版社系列答案
寒假作业重庆出版社系列答案
智乐文化寒假作业期末综合复习东南大学出版社系列答案
寒假作业轻松快乐每一天系列答案
 定义域为
定义域为 (
( ),设
),设 .
.
(1)试确定 的取值范围,使得函数
的取值范围,使得函数 在
在 上为单调函数;
上为单调函数;
(2)求证: ;
;
(3)求证:对于任意的 ,总存在
,总存在 ,满足
,满足 ,并确定这样的
,并确定这样的 的个数.
的个数. ,
, .
.
(Ⅰ)当 时,
时, 在
在 上恒成立,求实数
上恒成立,求实数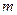 的取值范围;
的取值范围;
(Ⅱ)当 时,若函数
时,若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值
的取值 范围;
范围;
(Ⅲ)是否存在实数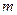 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出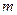 的值,若不存在,说明理由.
的值,若不存在,说明理由. ,其中a为常数.
,其中a为常数.
(I)若x=1是函数 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)若函数 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(III)若函数 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成
本为6万元.该建筑物每年的能源消耗费用C(单位:万 元)与隔热层厚度x(单位:cm)
元)与隔热层厚度x(单位:cm)
满足两个关系:①C(x)= ②若不建隔热层,每年能源消耗费用为8万
②若不建隔热层,每年能源消耗费用为8万
元。设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求k的值及f(x)的表达式; (4分)
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号