Question

2．角α=x，且0＜x＜$\frac{π}{2}$，于是x，sinx，tanx都是实数，请你给x一个具体的值，比较这三个实数的大小，并且判断得到的大小关系是否对区间（0，$\frac{π}{2}$）上都成立，为什么？

Answer 1

分析 分别取x=$\frac{π}{6}$，x=$\frac{π}{3}$，计算sinx和tanx比较大小，理由三角函数线得出结论．

解答 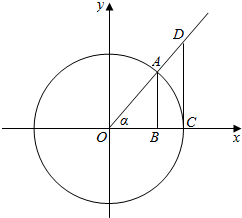解：当x=$\frac{π}{6}$时，sinx=$\frac{1}{2}$，tanx=$\frac{\sqrt{3}}{3}$，此时有sinx＜x＜tanx．
sinx＜x＜tanx在（0，$\frac{π}{2}$）上一定成立．
理由如下：
作单位圆O，设α终边与单位圆交于点A，过A作AB⊥x轴于B，过单位点C（1，0）作CD⊥x轴交α终边于D．
则AB=sinα=sinx，CD=tanα=tanx，$\widehat{AC}$=α=x，
由图可知S_△OAC＜S_扇形OAC＜S_△OCD，
∴$\frac{1}{2}×OC×AB$＜$\frac{1}{2}×OC×\widehat{AC}$＜$\frac{1}{2}×OC×CD$，
∴AB＜$\widehat{AC}$＜CD，即sinx＜x＜tanx在（0，$\frac{π}{2}$）上恒成立．

点评 本题考查了三角函数的大小比较，作出三角函数线是解题的关键．