
【题目】在如图所示的三棱锥![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 是
是![]() 的中位线,
的中位线,![]() 为线段
为线段![]() 的中点.
的中点.
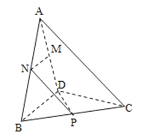
(1)证明:![]() .
.
(2)若二面角![]() 为直二面角,求二面角
为直二面角,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图,由中位线可得![]() ,取
,取![]() 的中点为
的中点为![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证
,可证![]() 平面
平面![]() ,从而可证
,从而可证![]() .
.
(2)建立如图所示的空间直角坐标系,计算出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量的夹角的余弦值后可得二面角
的法向量的夹角的余弦值后可得二面角![]() 的余弦值.
的余弦值.
(1)如图,取![]() 的中点为
的中点为![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,所以
,所以![]() .
.
因为![]() ,故
,故![]() ,故
,故![]() .
.
因为![]() ,所以
,所以![]() 且
且![]() ,所以
,所以![]() .
.
因为![]() ,故
,故![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,![]()
![]() .
.
因为![]() ,故
,故![]() ,所以
,所以![]() .
.

(2)由(1)可得![]() ,
,![]()
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
因为二面角![]() 为直二面角,所以
为直二面角,所以![]() 即
即![]() .
.
建立如图所示的空间直角坐标系,
则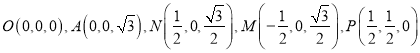 .
.
故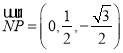 ,
, ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则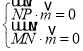 即
即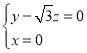 ,故
,故![]() ,取
,取![]() ,则
,则![]() ,
,
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则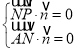 即
即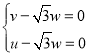 ,取
,取![]() ,则
,则![]() ,
,
故![]() ,
,
所以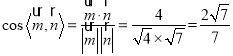 ,
,
因为二面角![]() 的平面角为锐角,
的平面角为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() ,
,![]() 、
、![]() 分别为
分别为![]() 的外心,重心,
的外心,重心,![]() .
.
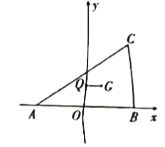
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点且满足
两点且满足![]() ,若存在求出
,若存在求出![]() 的方程,若不存在请说明理由.
的方程,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某口罩厂一年中各月份的收入、支出情况如图所示(单位:万元,下列说法中错误的是(注:月结余=月收入一月支出)( )
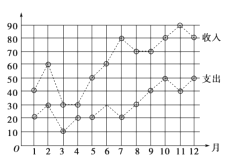
A.上半年的平均月收入为45万元B.月收入的方差大于月支出的方差
C.月收入的中位数为70D.月结余的众数为30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右焦点为
的右焦点为![]() ,下顶点为P,过点
,下顶点为P,过点![]() 的动直线l交椭圆C于A,B两点.
的动直线l交椭圆C于A,B两点.
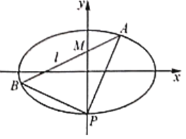
(1)当直线l平行于x轴时,P,F,A三点共线,且![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)当椭圆C的离心率为何值时,对任意的动直线l,总有![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增进市民的环保意识,某市有关部门面向全体市民进行了一次环保知识的微信问卷测试活动,每位市民仅有一次参与问卷测试机会.通过抽样,得到参与问卷测试的1000人的得分数据,制成频率分布直方图如图所示.

(1)估计成绩得分落在[86,100]中的概率.
(2)设这1000人得分的样本平均值为![]() .
.
(i)求![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(ii)有关部门为参与此次活动的市民赠送20元或10元的随机话费,每次获赠20元或10元的随机话费的概率分别为![]() 和
和![]() .得分不低于
.得分不低于![]() 的可获赠2次随机话费,得分低于
的可获赠2次随机话费,得分低于![]() 的可获赠1次随机话费.求一位市民参与这次活动获赠话费
的可获赠1次随机话费.求一位市民参与这次活动获赠话费![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() .给出以下四个命题:
.给出以下四个命题:
①平面![]() 与平面
与平面![]() 所成角的最大值为45°;
所成角的最大值为45°;
②四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
③四棱锥![]() 的体积为
的体积为![]() ;
;
④点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() .
.
其中命题正确的序号为( )
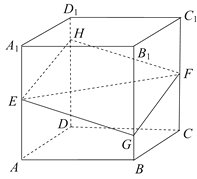
A.②③④B.②③C.①②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com