
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
分析 由已知中的不等式|x+3|+|x-1|<a2-3a,我们可以构造绝对值函数,根据绝对值的几何意义,我们易求出对应函数y=|x+3|+|x-1|的值域,进而得到实数a的取值范围.
解答 解:令y=|x+3|+|x-1|
则函数y=|x+3|+|x-1|≥|x+3-x+1|=4,
∴函数的值域为[4,+∞)
若不等式|x+3|+|x-1|<a2-3a有解,
则a2-3a>4,解得:a>4或a<-1,
故实数a的取值范围是(-∞,-1)∪(4,+∞),
故选:A.
点评 本题考查的知识点是绝对值三角不等式,其中构造绝对值函数,并根据绝对值的几何意义,判断出函数y=|x+3|+|x-1|的值域是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若α⊥β,a?α,b?β,则a⊥b | ||
| C. | 若a⊥b,b⊥α,则a∥α | D. | 若α∥β,a?α,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
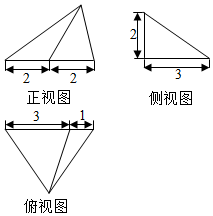
| A. | 4cm | B. | $\sqrt{13}$cm | C. | $\sqrt{14}$cm | D. | $\sqrt{15}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com