
 如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 | ||
|
| 5 |
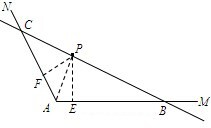 解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.
解:过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 2 | ||
|
| 1 |
| 2 |
| 2 | ||
|
| 1 |
| 2 |
| 2 | ||
|
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
15
|
15
|
| 5 |
| 5 |
| 5 |
| 1 |
| 2 |
| 2 | ||
|


科目:高中数学 来源: 题型:
| f(a)+f(b) |
| a+b |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| |MN| |
| |AB| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com