
���� ��I������$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\\{{��}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$�ɰ�ԲC�ļ����귽�̻�Ϊ��ͨ���̣�
��II����ȥ������ֱ��l�IJ������̻�Ϊ��ͨ���̣����Բ��C��ֱ��l�ľ���d���ó�ֱ����Բ��λ�ù�ϵ���ɵó���
��� �⣺��1������C�ļ����귽��Ϊ��=2sin�ȣ��ȡ�[0��2�У�������2=2��sin�ȣ���Ϊx2+y2-2y=0���䷽Ϊx2+��y-1��2=1��
��2������C��Բ��C��0��1�����뾶r=1��
ֱ��l��$\left\{\begin{array}{l}{x=\sqrt{3}t+\sqrt{3}}\\{y=3t+2}\end{array}\right.$����tΪ������t��R����Ϊ��ͨ���̣�$\sqrt{3}x$-y-1=0��
�ɵ�Բ��C��ֱ��l�ľ���d=$\frac{|0-1-1|}{2}$=1=0��
��ֱ��l��ԲC���У����е㼴Ϊ����
����$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-2y=0}\\{\sqrt{3}x-y-1=0}\end{array}\right.$�����D$��\frac{\sqrt{3}}{2}��\frac{1}{2}��$��
���� ���⿼���˲������̻�Ϊ��ͨ���̡������귽�̻�Ϊֱ�����귽�̡��㵽ֱ�ߵľ��빫ʽ��ֱ����Բ�������⣬������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | 10 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {-1��1} | C�� | {-1��1��2} | D�� | {1��0} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
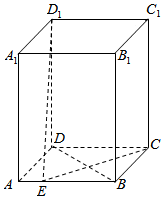 ��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������
��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������| A�� | $2\sqrt{2}$ | B�� | $\sqrt{10}$ | C�� | $\sqrt{5}+1$ | D�� | $2+\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com