
分析 (1)利用相互独立事件乘法概率公式求解.
(2)利用对立事件概率乘法公式求解.
解答 解:(1)甲,乙两个气象台独立预报天气准确的概率分别为$\frac{4}{5}$和$\frac{3}{4}$,
∴甲、乙两个气象台同时预报天气准确的概率:
p1=$\frac{4}{5}×\frac{3}{4}$=$\frac{3}{5}$.
(2)至少有一个气象台预报准确的概率:
p2=1-(1-$\frac{4}{5}$)(1-$\frac{3}{4}$)=$\frac{19}{20}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意相互独立事件乘法概率公式、对立事件概率公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {-1,1,2} | C. | {0,1,2,3} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
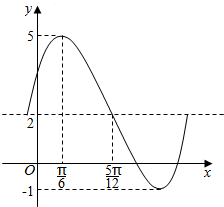 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车次 | 芜湖发车 | 到达马鞍山东 | 耗时 |
| G7174 | 13:37 | 14:02 | 25分钟 |
| G7178 | 15:05 | 15:24 | 19分钟 |
| D5606 | 15:37 | 16:02 | 25分钟 |
| D5608 | 17:29 | 17:48 | 19分钟 |
| G7088 | 18:29 | 18:48 | 19分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2:1 | B. | 3:1:2 | C. | 6:1:2 | D. | 6:2:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com