考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
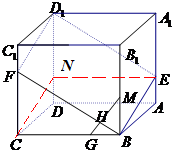
分析:(Ⅰ)在DD1上取一点N使得DN=1,连结CN,EN,得到四边形CFD1N是平行四边形,四边形DNEA是平行四边形,由此能够证明E,B,F,D1四点共面.
(Ⅱ)由已知条件推导出△BCF∽△MBG,从而推导出四边形ABME是矩形,由此能够证明EM⊥面BCC1B1.
(Ⅲ)由已知条件推导出∠MHE就是截面EBFD1和面BCC1B1所成锐二面角的平面角,由此能求出结果.
解答:
(Ⅰ)证明:在DD
1上取一点N使得DN=1,
连接CN,EN,显然四边形CFD
1N是平行四边形,
∴D
1F∥CN.同理四边形DNEA是平行四边形,
∴EN∥AD,且EN=AD.又BC∥AD,且AD=BC,
∴EN∥BC,EN=BC,∴四边形CNEB是平行四边形.
∴CN∥BE.∴D
1F∥BE.
∴E,B,F,D
1四点共面.….(5分)
(Ⅱ)证明:∵GM⊥BF,∴△BCF∽△MBG,
∴
=,即
=.∴MB=1.….(7分)
∵AE=1,∴四边形ABME是矩形.∴EM⊥BB
1.….(8分)
又∵平面ABB
1A
1⊥平面BCC
1B
1,且EM在平面ABB
1A
1内,
∴EM⊥面BCC
1B
1.….(10分)
(Ⅲ)∵EM⊥面BCC
1B
1,∴EM⊥BF,EM⊥MH,GM⊥BF.
∴∠MHE就是截面EBFD
1和面BCC
1B
1所成锐二面角的平面角.….(12分)
∵∠EMH=90°,∴tanθ=
,ME=AB=3,△BCF∽△MHB.
∴3:MH=BF:1.又∵BF=
=
,
∴MH=
.∴tanθ=
=.
所以
cosθ=.…..(14分)
点评:本题考查四点共面的证明,考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.

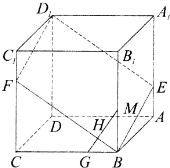 如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=F1C=1.
如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=F1C=1.


 作业辅导系列答案
作业辅导系列答案 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.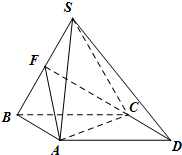 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.