
分析 由题意可知:an+1-an=2n+1,采用累加法即可求得数列an=n2,则bn=an-1=n2-1=(n+1)(n-1),当n≥2时,则$\frac{1}{{b}_{n}}$=$\frac{1}{(n-1)(n+1)}$=$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),采用“裂项法”即可求得实数m的取值范围.
解答 解:由an+1=an+2n+1,则an+1-an=2n+1,
则a2-a1=3,
a3-a2=5,
a4-a3=7,
…
an-an-1=2n-1,
以上各式相加:an-a1=3+5+7+…+2n-1=$\frac{(3+2n-1)(n-1)}{2}$=n2-1,
an=n2-1+a1=n2,
当n=1时成立,
∴an=n2,
bn=an-1=n2-1=(n+1)(n-1),
当n≥2时,则$\frac{1}{{b}_{n}}$=$\frac{1}{(n-1)(n+1)}$=$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),
$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{n-2}$-$\frac{1}{n}$)+$\frac{1}{2}$($\frac{1}{n-1}$-$\frac{1}{n+1}$),
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n}$-$\frac{1}{n+1}$)<$\frac{3}{4}$,
由$\frac{1}{b_2}+\frac{1}{b_2}+…+\frac{1}{b_n}<m$,则$m≥\frac{3}{4}$,
实数m的取值范围[$\frac{3}{4}$,+∞),
故答案为:[$\frac{3}{4}$,+∞).
点评 本题考查“累加法”求数列的通项公式,“错位相减法”求数列的前n项和,考查数列与不等式的综合应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
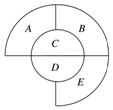 已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.
已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+3i | B. | 3-i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{5}{18}$ |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com