
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
分析 (1)利用平均数公式计算即得;
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图;
(3)作出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,再求出a的值,即可求出回归方程.
解答 解:(1)求$\overline x$=$\frac{1}{7}×(3+4+5+6+7+8+9)$=6,
$\overline y$=$\frac{1}{7}×(66+69+73+81+89+90+91)$=79.86;
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
散点图如下图所示.
(3)由散点图知,y与x有线性相关关系,设线性回归方程为$\widehaty=bx+a$,
∵$\sum_{i=1}^7{x_i^2}=280$,$\sum_{i=1}^7{y_i^2}=45309$,$\sum_{i=1}^7{{x_i}{y_i}}=3487$,$\overline x=6$,$\overline y=79.86$,
∴$b=\frac{{3487-7×6×\frac{559}{7}}}{280-7×36}=\frac{133}{28}=4.75$,a=79.86-6×4.75=51.36,
∴线性回归方程为$\widehaty=4.75x+51.36$.
点评 本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法做出线性回归方程的系数,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
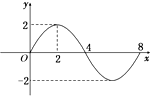 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )| A. | $\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
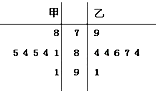 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com