
分析 (1)求出二次函数的对称性,讨论对称性和$\frac{1}{2}$的关系进行求解就可.
(2)根据不等式恒成立转化为不等式组关系,利用线性规划的知识进行求解.
解答 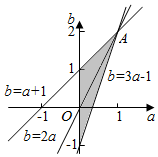 解:(1)(i)∵a>0,b∈R,
解:(1)(i)∵a>0,b∈R,
∴抛物线开口向上,对称性x=$\frac{b}{4a}$,
当$\frac{b}{4a}$≤$\frac{1}{2}$,即b≤2a时,f(x)max=f(1)=3a-
当$\frac{b}{4a}$>$\frac{1}{2}$,即b>2a时,f(x)max=f(0)=-a+b,
则f(x)max=$\left\{\begin{array}{l}{3a-b,}&{b≤2a}\\{-a+b,}&{b>2a}\end{array}\right.$=|2a-b|+a;
(ii)当b≤2a时,f(x)+|2a-b|+a=4ax2-2bx+2a≥4ax2-4ax+2a=2a(2x2-2x+1);
$\begin{array}{l}当b>2a时,f(x)+|2a-b|+a=4a{x^2}+2b(1-x)-2a≥4a{x^2}+4a(1-x)-2a=2a(2{x^2}-2x+1),\\ 令g(x)=2{x^2}-2x+1=2{(x-\frac{1}{2})^2}+\frac{1}{2}>0,故f(x)+|2a-b|+a≥2a•g(x)≥0\end{array}$
(2)由(i)知,当0≤x≤1,f(x)max=|2a-b|+a,
∴f(x)max=|2a-b|+a≤1;若|2a-b|+a≤1;
则由(ii)知f(x)≥-(|2a-b|+a)≥-1; …(10分)
则-1≤f(x)≤1对任意x∈[0,1]恒成立的等价条件是$\left\{\begin{array}{l}{|2a-b|+a≤1}\\{a>0}\end{array}\right.$,即$\left\{\begin{array}{l}{2a-b≥0}\\{3a-b≤1}\\{a>0}\end{array}\right.$,或$\left\{\begin{array}{l}{2a-b<0}\\{b-a≤1}\\{a>0}\end{array}\right.$(•) …(12分)
在直角坐标系aob 中,(*)所表示的平面区域为下图,所以a+b的范围是(-1,3]…(15分)
点评 本题主要考查不等式恒成立问题,涉及一元二次函数的性质故,根据条件关系转化为线性规划是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{2}}}{9}$ | B. | $\frac{2}{9}$ | C. | $-\frac{2}{9}$ | D. | $-\frac{{4\sqrt{2}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
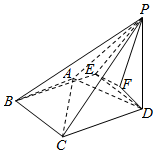 如图所示的四棱 P-ABCD中,AB=BC=$\sqrt{2}$,AD=DC=$\sqrt{5}$,PD=2,AB⊥BC,E,F分别是△PAC与△PCD的重心.
如图所示的四棱 P-ABCD中,AB=BC=$\sqrt{2}$,AD=DC=$\sqrt{5}$,PD=2,AB⊥BC,E,F分别是△PAC与△PCD的重心.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
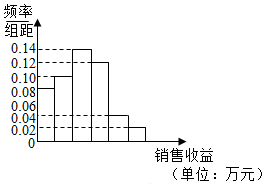 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com