
分析 分别求出p,¬p以及¬q的范围,根据p,q的真假,得到关于x的不等式组,解出即可.
解答 解:由lg(x2-2x-2)≥0,得x2-2x-2≥1,
∴x≥3,或x≤-1.即p:x≥3,或x≤-1,
∴非p:-1<x<3.又∵q:0<x<4,
∴非q:x≥4,或x≤0,
由p且q为假,p或q为真知p、q一真一假.
当p真q假时,由$\left\{\begin{array}{l}{x≥3或x≤-1}\\{x≥4或x≤0}\end{array}\right.$,得x≥4,或x≤-1.
当p假q真时,由$\left\{\begin{array}{l}{-1<x<3}\\{0<x<4}\end{array}\right.$,得0<x<3.
综上知,实数x的取值范围是{x|x≤-1,或0<x<3,或x≥4}.
点评 本题考查了对数函数以及复合命题的真假,考查分类讨论思想,是一道基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,2,3} | C. | {4,5} | D. | {3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
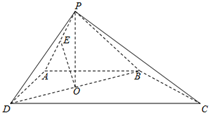 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-36°,54°} | B. | {-126°,144°} | ||
| C. | {-36°,54°,-126°,144°} | D. | {54°,-126°} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com