
分析 (1)设每期须还x万元,由题意可得x(1+r)4+ x(1+r)3+…+x= a(1+r)5,解得即可,
(2)设每期须还x万元,由题意得x(1+4r)+ x(1+3r)+…+x= a(1+5r),解得即可.
解答 解:(1)设每期须还x万元,则第一期还x万元,到结账时相当于x(1+r)4万元;
第二期还x万元,到结账时相当于x(1+r)3万元;…第五期还x万元,到结账时仍是x万元.
因为五期总和为a万元在银行存五期的本息之和为a(1+r)5,
从而x(1+r)4+ x(1+r)3+…+x= a(1+r)5,
解得x=$\frac{ar(1+r)^{5}}{(1+r)^{5}-1}$,
(2)设每期须还x万元,则第一期还x万元,到结账时相当于x(1+4r)万元; 第二其还x万元,到结账时相当于x(1+3r)万元;…第五期还x万元,到结账时仍为x万元.因为五期总和为a万元在银行存五期的本息之和为a(1+5r),
从而利用x(1+4r)+ x(1+3r)+…+x= a(1+5r),
解得,x=$\frac{a(1+5r)}{5+10r}$.
点评 本题考查了数列在分期还款中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 30° | C. | 135° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
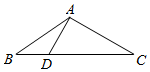 如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.
如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC=$\frac{\sqrt{6}}{3}$,AB=6,BD=$\sqrt{6}$,则ADsin∠BAD=.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
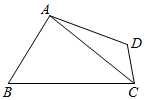 如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.
如图,在四边形ABCD中,∠ABC=$\frac{π}{3}$,AB:BC=2:3,$AC=\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
| 组别 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com