考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:几何法:
(1)设A
1B∩AB
1=Q,连结PQ.由已知条件推导出PQ⊥AB
1.PQ⊥A
1B.从而得到PQ⊥平面ABB
1A
1.由此能证明平面APB
1⊥平面ABB
1A
1.
(2)设AB=AA
1=2,求出
S△APB1=
,S
△ABC=
,由此能求出平面APB
1与平面ABC所成锐二面角的余弦值.
向量法:
(1)以A为原点建立空间直角坐标系A-xyz,并设AB=a,AA
1=b,由此利用向量法能证明面APB
1⊥面ABB
1A
1.
(2)设a=b=1,分别求出平面APB
1的一个法向量和平面ABC的一个法向量,由此利用向量法能证明平面PAB
1与平面ABC所成锐二面角的余弦值.
解答:
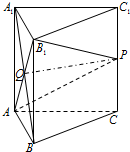
几何法:
(1)证明:设A
1B∩AB
1=Q,连结PQ.
∵P是CC
1的中点,∴AP=B
1P,
又Q是A
1B
1中点,∴PQ⊥AB
1.
同理可证PQ⊥A
1B.∴PQ⊥平面ABB
1A
1.
又PQ?平面APB
1,∴平面APB
1⊥平面ABB
1A
1.
(2)解:不妨设AB=AA
1=2,
则
AQ=,PA=,
PQ=,
∴
S△APB1=
×AB1×PQ=AQ×PQ=×=.
又S
△ABC=
×2×2×sin60°=
,
∴平面APB
1与平面ABC所成锐二面角的余弦值为
==.
向量法:
(1)证明:如图,以A为原点建立空间直角坐标系A-xyz,并设AB=a,AA
1=b
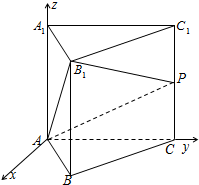
则A(0,0,0),
B=(,,0),
B1=(,,b)P(0,a,).
=
(,,0),
=
(,,b)=
(0,a,).
设向量
=(1,x,y)是平面ABB
1的一个法向量,
则
•=
(1,x,y)•(,,0)=+=0,
•=
(1,x,y)•(,,b)=++by=0解得:
x=-,y=0,∴
=(1,-,0),
又设
=(x0,y0,1)是平面APB
1的一个法向量,
则
•=
(x0,y0,1)•(0,a,)=
ay0+=0,
•=
(x0,y0,1)•(,,b)=x0+y0+b=0,
解得
x0=-,
y0=-,∴
=
(-,-,1),
∴
•=
(1,-,0)•(-,-,1)=0.
∴平面APB
1⊥平面ABB
1A
1.
(2)解:不妨设a=b=1,则平面APB
1的一个法向量
=
(-,-,1).
又平面ABC的一个法向量是
=(0,0,1),
∵
cos<,>=
=
=,
∴平面PAB
1与平面ABC所成锐二面角的余弦值为
.
点评:本题考查平面与平面垂直的证明,考查平面与平面所成锐二面角的求法,解题时要认真审题,注意空间思维能力的培养.

 如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.
如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点. 几何法:
几何法: 则A(0,0,0),B=(
则A(0,0,0),B=(

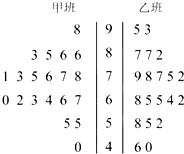 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.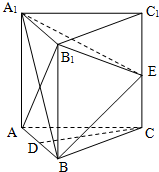 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.