
| A. | (2,1) | B. | (-2,1) | C. | $({-1,\frac{1}{4}})$ | D. | $({1,\frac{1}{4}})$ |
分析 过点P作PN⊥l,连接FP,利用抛物线的定义可得|PN|=|FP|.,可知当PQ∥y轴时,点P、Q、N三点共线,因此,|PQ|+|PF|取得最小值|QN|,求出即可.
解答 解:抛物线x2=4y的焦点F的坐标为F(0,1),准线方程为y=-1,
过点P作PN⊥l,垂足为N,连接FP,则|PN|=|FP|.
故当PQ∥y轴时,|PQ|+|PF|取得最小值|QN|=2-(-1)=3.
设点P(1,y),代入抛物线方程12=4y,解得y=$\frac{1}{4}$,
∴P(1,$\frac{1}{4}$).
故选D.
点评 本题考查抛物线的简单性质,着重考查抛物线的定义的应用,突出转化思想的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{e}{3}$,+∞) | B. | [$\frac{e}{3}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
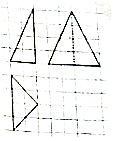 一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )| A. | 16π | B. | 32π | C. | 48π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | e2<x3x4<(2e-1)2 | C. | 0<(2e-x3)(2e-x4)<1 | D. | 1<x1x2<e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n2+2n | B. | n2+2n | C. | 2n2+n | D. | 2(n2+2n) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com