Question

3．已知△ABC是直角三角形，斜边BC的中点为M，试建立适当的直角坐标系，证明：|AM|=$\frac{1}{2}$|BC|．

Answer 1

分析 通过建立平面直角坐标系，设出B、C坐标，利用中点坐标公式以及距离公式求解即可．

解答 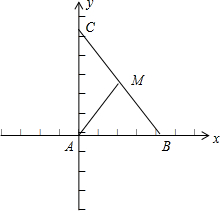解：如图：设B（a，0），C（0，b），由中点坐标公式可得M（$\frac{a}{2}，\frac{b}{2}$），
则|AM|=$\sqrt{（\frac{a}{2}）^{2}+（\frac{b}{2}）^{2}}$=$\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}$．
$\frac{1}{2}$|BC|=$\frac{1}{2}$$\sqrt{{（a-0）}^{2}+{（0-b）}^{2}}$=$\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}$．
∴|AM|=$\frac{1}{2}$|BC|．

点评 本题考查解析法证明平面集合问题，两点间距离公式的应用，考查计算能力．