
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
分析 由cos α=cos β得到α与β的关系判断①;求出函数y=2cos$\frac{x}{3}$的对称轴方程判断②;利用偶函数的定义判断③;画出函数的图象判断④.
解答 解:对于①,若cos α=cos β,则α-β=2kπ,k∈Z或α+β=2kπ,k∈Z,故①错误;
对于②,由$\frac{x}{3}=kπ$,得x=3kπ,k∈Z,
∵3kπ$≠\frac{π}{12}$,∴函数y=2cos$\frac{x}{3}$的图象不关于x=$\frac{π}{12}$对称,故②错误;
对于③,由cos[sin(-x)]=cos(-sinx)=cos(sinx),得函数y=cos(sin x)(x∈R)为偶函数,故③正确;
对于④,函数y=sin|x|=$\left\{\begin{array}{l}{sinx,x≥0}\\{-sinx,x<0}\end{array}\right.$,
其图象如图,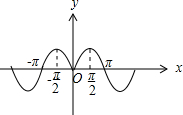
由图可知,函数不是周期函数,故④错误.
∴不正确的命题是①②④.
故选:D.
点评 本题考查命题的真假判断与应用,考查了三角函数的图象和性质,属中档题.


科目:高中数学 来源: 题型:选择题
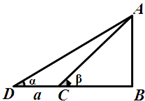 如图所示,D,C,B三点在地面的同一直线上,CD=a,从D,C两点测得A的仰角分别是α,β(α<β),则点A离地面的高AB等于( )
如图所示,D,C,B三点在地面的同一直线上,CD=a,从D,C两点测得A的仰角分别是α,β(α<β),则点A离地面的高AB等于( )| A. | $\frac{acosαcosβ}{cos(β-α)}$ | B. | $\frac{acosαcosβ}{sin(β-α)}$ | C. | $\frac{asinαsinβ}{cos(β-α)}$ | D. | $\frac{asinαsinβ}{sin(β-α)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
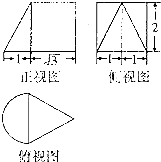
| A. | $\frac{π}{3}$+2$\sqrt{3}$ | B. | $\frac{π}{3}$+$\sqrt{3}$ | C. | π+2$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 20 | C. | 30 | D. | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y-4=0 | B. | 2x+y-4=0 | C. | 2x+3y+4=0 | D. | x+2y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com