
分析 以直三棱锥为模型即可判断①错误;以平行六面体为模型可判断②正确;利用等体积法即可求出正四面体内切球的半径,继而得出内切球的面积;由线面垂直的判定与性质可证P在底面的投影为△ABC的垂心,根据线面垂直即可证出结论成立.
解答 解:对于①,以直三棱柱为模型,三棱柱的两个侧面都与底面垂直,但侧面不平行,故①错误
对于②,在a、b、c上取三条线段AB、CC′、A′D′,
作一个平行六面体ABCD-A′B′C′D′,如右图所示
在c上,即在直线A′D′上取一点P,过a、P作一个平面β
平面β与DD′交于Q、与CC′交于R,
由面面平行的性质定理,得QR∥a,
于是PR不与a平行,但PR与a共面.故PR与a相交,得直线PR是与a,b,c都相交的一条直线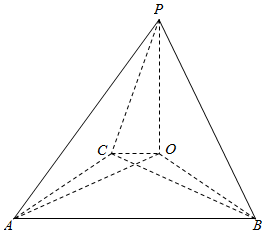
根据点P的任意性,得与a,b,c都相交的直线有无穷多条.故②正确.
对于③,设正三棱锥内切球心为O,半径为r,连结OP,OA,OB,OC.则球心O到各面的距离均为r.
∴VP-ABC=$\frac{1}{3}{S}_{O-ABC}•r$×4=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}•r×4$=$\frac{\sqrt{3}}{3}{a}^{2}r$.
∵三棱锥P-ABC为棱长为a的正四面体,∴棱锥的高h=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{2}a×\frac{2}{3})^{2}}$=$\frac{\sqrt{6}}{3}a$.
∴VP-ABC=$\frac{1}{3}{S}_{△ABC}•h$=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×\frac{\sqrt{6}}{3}a$=$\frac{\sqrt{2}{a}^{3}}{12}$.
∴$\frac{\sqrt{3}}{3}{a}^{2}r$=$\frac{\sqrt{2}{a}^{3}}{12}$.
解得r=$\frac{\sqrt{6}a}{12}$.
∴内切球的面积S=4πr2=4$π×\frac{6{a}^{2}}{144}$=$\frac{π{a}^{2}}{6}$.故③正确.
对于④,过P作平面ABC的垂线PO,连结OA,OB,OC
则PO⊥BC,又PA⊥BC,故BC⊥平面PAO,于是BC⊥OA,
同理可证AC⊥OB,
所以O是△ABC的垂心,于是AB⊥CO,
又AB⊥PO,于是AB⊥平面PCO,所以PC⊥AB,故④正确.
故答案为②③④.
点评 本题考查了空间项目位置关系的判断,平面的性质,多面体与内切球的关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | $(0,\frac{1}{2})$ | C. | $[\frac{1}{2},1)$ | D. | $(0,\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
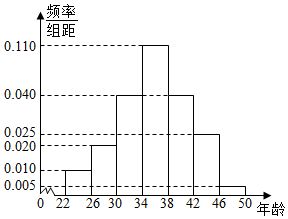 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下;
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com