Question

2．如图，三棱柱ABC-A₁B₁C₁中，侧棱AA₁⊥底面ABC，AA₁=2，AB=BC=1，∠ABC=90°，外接球的球心为O，点E是侧棱BB₁上的一个动点．有下列判断：
①直线AC与直线C₁E是异面直线；②A₁E一定不垂直于AC₁；③三棱锥E-AA₁O的体积为定值；④AE+EC₁的最小值为2$\sqrt{2}$．
其中正确的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由题意画出图形，由异面直线的概念判断①；利用线面垂直的判定与性质判断②；找出球心，由棱锥底面积与高为定值判断③；设BE=x，列出AE+EC₁关于x的函数式，结合其几何意义求出最小值判断④．

解答 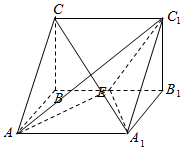解：如图，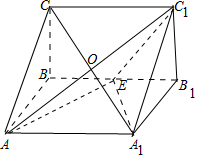

对于①，∵直线AC经过平面BCC₁B₁内的点C，而直线C₁E在平面BCC₁B₁内不过C，∴直线AC与直线C₁E是异面直线，故①正确；
对于②，当E与B重合时，AB₁⊥A₁B，而C₁B₁⊥A₁B，∴A₁B⊥平面AB₁C₁，则A₁E垂直AC₁，故②错误；
对于③，由题意知，直三棱柱ABC-A₁B₁C₁的外接球的球心为O是AC₁ 与A₁C 的交点，则△AA₁O的面积为定值，由BB₁∥平面AA₁C₁C，∴E到平面AA₁O的距离为定值，∴三棱锥E-AA₁O的体积为定值，故③正确；
对于④，设BE=x，则B₁E=2-x，∴AE+EC₁=$\sqrt{1+{x}^{2}}+\sqrt{1+（2-x）^{2}}$．由其几何意义，即平面内动点（x，1）与两定点（0，0），（2，0）距离和的最小值知，其最小值为2$\sqrt{2}$，故④正确．
∴正确命题的个数是3个．
故选：C．

点评 本题考查命题的真假判断与应用，考查空间想象能力和思维能力，属中档题．