
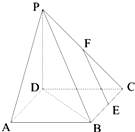
 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.| 2 |
| PD |
| BD |
| ||
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
| A、(-1,1) |
| B、[-1,1) |
| C、[-1,1] |
| D、(-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+λ |
| 3n |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:
某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告:| 广告一 | 广告二 | |||
| 回答正 确人数 |
占本组 人数频率 |
回答正 确人数 |
占本组 人数频率 | |
| [10,20) | 90 | 0.5 | 45 | a |
| [20,30) | 225 | 0.75 | k | 0.8 |
| [30,40) | b | 0.9 | 252 | 0.6 |
| [40,50) | 160 | c | 120 | d |
| [50,60] | 10 | e | f | g |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com