
分析 通过记第n年维修费用为an,计算可知an=0.1n+0.1(万元),进而可知前n年维修费用An=$\frac{n(0.1n+0.3)}{2}$(万元),化简可知年平均费用S=$\frac{10}{n}$+$\frac{0.1n}{2}$+$\frac{2.3}{2}$,进而利用基本不等式计算即得结论.
解答 解:依题意,记第n年维修费用为an,则an=0.2+0.1(n-1)=0.1n+0.1(万元),
则前n年维修费用An=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{n(0.2+0.1n+0.1)}{2}$=$\frac{n(0.1n+0.3)}{2}$(万元),
故年平均费用S=$\frac{10+{A}_{n}+n}{n}$=$\frac{10}{n}$+$\frac{0.1n}{2}$+$\frac{2.3}{2}$,
∵$\frac{10}{n}$+$\frac{0.1n}{2}$≥2$\sqrt{\frac{10}{n}•\frac{0.1n}{2}}$=$\sqrt{2}$,
当且仅当$\frac{10}{n}$=$\frac{0.1n}{2}$即n=10$\sqrt{2}$时取等号,
∴这种汽车使用10$\sqrt{2}$年时,它的年平均费用最少,
故答案为:10$\sqrt{2}$.
点评 本题考查函数模型的选择与应用,考查等差数列的求和,考查基本不等式,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
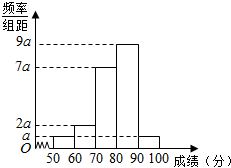 某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图
某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| Q(x)(台) | 6 | 9 | 10 | 8 | 6 | 2 |
| A. | Q(x)=ax+b(a≠0) | B. | Q(x)=a|x-4|+b(a≠0) | ||
| C. | Q(x)=a(x-3)2+b(a≠0) | D. | Q(x)=a•bx(a≠0,b>0且b≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $({0,\frac{1}{2}})$ | C. | $({0,\frac{1}{4}})$ | D. | $({0,\frac{1}{8}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com