
分析 运用向量数量积的定义和性质,可得|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{19}$,再由向量数量积的定义和余弦函数的值域,即可得到所求最大值.
解答 解:|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,
可得|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=4+9+2×2×3×$\frac{1}{2}$=19,
即有|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{19}$,
则($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{e}$=|$\overrightarrow{a}$+$\overrightarrow{b}$|•|$\overrightarrow{e}$|•cos<($\overrightarrow{a}$+$\overrightarrow{b}$),$\overrightarrow{e}$>
=$\sqrt{19}$cos<($\overrightarrow{a}$+$\overrightarrow{b}$),$\overrightarrow{e}$>≤$\sqrt{19}$,
当cos<($\overrightarrow{a}$+$\overrightarrow{b}$),$\overrightarrow{e}$>=1,即($\overrightarrow{a}$+$\overrightarrow{b}$),$\overrightarrow{e}$同向共线时,
取得最大值$\sqrt{19}$.
故答案为:$\sqrt{19}$.
点评 本题考查向量数量积的定义和性质,主要是向量的平方即为模的平方,考查化简运算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
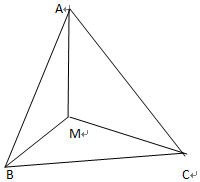 如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;
如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (2,6) | C. | (0,6) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com