
分析 设A中的最大数为k,其中1≤k≤n-1,整数n≥3,则A中必含元素k,另元素1,2,…,k-1,可在A中,B中必不含元素1,2,…,k;元素k+1,k+2,…,k可在B中,但不能都不在B中.由此能求出an.
解答 解:设A中的最大数为k,其中1≤k≤n-1,整数n≥3,
则A中必含元素k,另元素1,2,…,k-1,可在A中,
故A的个数为:${C}_{k-1}^{0}$+${C}_{k-1}^{1}$+…+${C}_{k-1}^{k-1}$=2k-1,
B中必不含元素1,2,…,k,
另元素k+1,k+2,…,n可在B中,但不能都不在B中,
故B的个数为:${C}_{n-k}^{1}$+${C}_{n-k}^{2}$+…+${C}_{n-k}^{n-k}$=2n-k-1,
从而集合对(A,B)的个数为2k-1•(2n-k-1)=2n-1-2k-1,
∴an=$\sum_{k=1}^{n-1}$(2n-1-2k-1)
=(n-1)•2n-1-$\frac{1-{2}^{n-1}}{1-2}$
=(n-2)•2n-1+1.
故答案为:(n-2)•2n-1+1.
点评 本题考查数列的第3项的求法,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
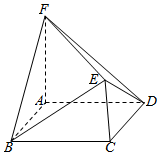 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com