
 如图,在四棱椎P-ABCD中,底面ABCD为矩形,平面PCD⊥面ABCD,BC=1,AB=2,PC=$PD=\sqrt{2}$,E为PA中点.
如图,在四棱椎P-ABCD中,底面ABCD为矩形,平面PCD⊥面ABCD,BC=1,AB=2,PC=$PD=\sqrt{2}$,E为PA中点.分析 (1)设AC与BD的交点为F,连结EF,推导出EF∥PC,由此能证明PC∥平面BED.
(2)取CD中点O,连接PO,PO⊥CD,则PO⊥平面ABCD.连接AO,取AO中点K,则$EK∥\frac{1}{2}PO=\frac{1}{2}$,且EK⊥平面ABCD,由此能出三棱锥E-PBD的体积.
解答 证明:(1)设AC与BD的交点为F,连结EF.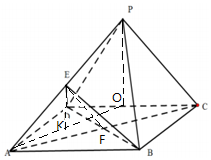
∵ABCD为矩形,所以F为AC的中点.
在△PAC中,由已知E为PA中点,
∴EF∥PC.
又EF?平面BED,PC?平面BED,
∴PC∥平面BED.
解:(2)取CD中点O,连接PO,PO⊥CD,平面PCD⊥平面ABCD,
∴PO⊥平面ABCD.
连接AO,取AO中点K,则$EK∥\frac{1}{2}PO=\frac{1}{2}$,且EK⊥平面ABCD.
∴三棱锥E-PBD的体积:
${V_{E-PBD}}={V_{P-ABCD}}-{V_{P-BCD}}=\frac{1}{3}×2×1×1-$$\frac{1}{3}×\frac{1}{2}×2×1×\frac{1}{2}-\frac{1}{3}×\frac{1}{2}×2×1×1=\frac{1}{6}$.
点评 本题考查几何体的体积的求法,考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50).[50,60),…,[90,100]后得到频率分布直方图(如图所示),则分数在[60,80)内的人数是45.
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50).[50,60),…,[90,100]后得到频率分布直方图(如图所示),则分数在[60,80)内的人数是45.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 矩形 | C. | 梯形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com