练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）在R上可导，且（x-1）•f′（x）＞0，则下列结论正确的是（　　）
    A、x=1一定是函数f（x）的极大值点
    B、x=1一定是函数f（x）的极小值点
    C、x=1不是函数f（x）的极值点
    D、x=1不一定是函数f（x）的极值点
    考点：利用导数研究函数的单调性
    专题：导数的综合应用
    分析：由条件判断函数的单调性，根据函数极值和导数之间的关系即可得到结论
    解答： 解：由（x-1）•f′（x）＞0得当x＞1时，f′（x）＞0，此时函数单调递增，
    当x＜1时，f′（x）＜0，此时函数单调递减，
    即x=1时，函数f（x）取得极小值，
    故选：B．
    点评：本题主要考查函数极值的判断，根据函数导数和单调性之间的关系是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设等差数列{an}的前n项和为Sn，若S9=72，则a1+a5+a9=（　　）
    A、36B、24C、16D、8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形，现将一粒豆子随机撒在第10个图中，则豆子落在白色地砖上的概率是（　　）
    A、
    10
    63
    B、
    10
    27
    C、
    17
    27
    D、
    53
    63

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    现有男生3人，女生5人，从男生中选2人，女生中选1人参加数学、物理、化学三科竞赛，要求每科均有1人参加，每名学生只参加一科竞赛，则不同的参赛方法共有（　　）种．
    A、15B、30C、90D、180

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    F1，F2是椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左、右焦点，若在椭圆上存在点P，且满足|PF1|=2|PF2|，则椭圆的离心率的取值范围为（　　）
    A、[
    1
    3
    ，1）
    B、（
    1
    3
    ，1）
    C、（
    2
    3
    ，1）
    D、（0，
    1
    3
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有甲、乙两位射击运动员进行射击测试，每人各射击10次，图1、图2分别是甲、乙两人射击命中环数分布的条形图，由条形图判断下列命题正确的是（　　）
    A、总体上甲比乙的射击命中能力更强，但乙的稳定性更好
    B、总体上乙比甲的射击命中能力更强，但甲的稳定性更好
    C、总体上甲、乙两人的射击命中能力基本相当，但乙的稳定性更好
    D、总体上甲、乙两人的射击命中能力基本相当，但甲的稳定性更好

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}满足a1=
    1
    2
    ，an+1=1-
    1
    an
    ，那么a10=（　　）
    A、-1
    B、
    1
    2
    C、1
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为了检验“喜欢玩手机游戏与认为作业多”是否有关系，某班主任对班级的30名学生进行了调查，得到一个2×2列联表：
    认为作业多 认为作业不多 合计
    喜欢玩手机游戏 18 2
    不喜欢玩手机游戏 6
    合计 30
    （Ⅰ）请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程）；
    （Ⅱ）能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系？
    （Ⅲ）若从不喜欢玩手机游戏的人中随机抽取3人，则至少2人认为作业不多的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

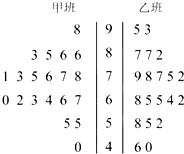    某次月考从甲、乙两班中各抽取20个物理成绩，整理数据得到茎叶图如图所示，根据茎叶图解决下列问题．
    （1）分别指出甲乙两班物理样本成绩的中位数；
    （2）分别求甲乙两班物理样板成绩的平均值；
    （3）定义成绩在80分以上为优秀，现从甲乙两班物理样本成绩中有放回地各随机抽取两次，每次抽取1个成绩，设ξ表示抽出的成绩中优秀的个数，求ξ的分布列及数学期望．

    查看答案和解析>>

    同步练习册答案