
分析 (1)先分类讨论,根据x的范围先去掉绝对值然后再根据绝对值不等式的解法进行求解.
(2)作出y=|x-3|+|x-4|与y=a的图象,使|x-3|+|x-4|<a解集为空集只须y=|x-3|+|x-4|图象在y=a的图象的上方,从而求出a的范围.
解答 解:(1)原不等式|x-3|+|x-4|<2
当x<3时,原不等式化为7-2x<2,解得x>$\frac{5}{2}$,∴$\frac{5}{2}$<x<3,
当3≤x≤4时,原不等式化为1<2,∴3≤x≤4
当x>4时,原不等式化为2x-7<2,解得x<$\frac{9}{2}$,∴4<x<$\frac{9}{2}$;
综上,原不等式解集为{x|$\frac{5}{2}$<x<$\frac{9}{2}$};(5分)
(2)法一、作出y=|x-3|+|x-4|与y=a的图象,
如图所示: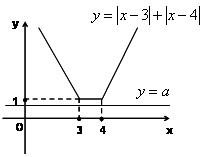
若使|x-3|+|x-4|<a解集为空集只须y=|x-3|+|x-4|图象在y=a的图象的上方,
或y=a与y=1重合,∴a≤1
所以,a的范围为(-∞,1],(10分)
法二、:y=|x-3|+|x-4|=$\left\{\begin{array}{l}{2x-7,x≥4}\\{1,3≤x≤4}\\{7-2x,x<3}\end{array}\right.$,
当x≥4时,y≥1
当3≤x<4时,y=1
当x<3时,y>1
综上y≥1,原问题等价为a≤[|x-3|+|x-4|]min
∴a≤1(10分)
法三、:∵|x-3|+|x-4|≥|x-3-x+4|=1,
当且仅当(x-3)(x-4)≤0时,上式取等号
∴a≤1.
点评 此题考查绝对值不等式的解法,运用了分类讨论的思想,解题的关键是去掉绝对值,此类题目是高考常见的题型.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com