在一次数学测验后,学习委员小明对选做题的选题情况进行了统计,如表:(单位:人)
|
几何证明选讲 |
坐标系与参数方程 |
不等式选讲 |
合计 |
| 男同学 |
12 |
4 |
6 |
22 |
| 女同学 |
0 |
8 |
12 |
20 |
| 合计 |
12 |
12 |
18 |
42 |
(Ⅰ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从选做不同选做题的同学中随机选出7名同学进行座谈.已知学习委员小明和两名数学科代表三人都在选做《不等式选讲》的同学中.求在这名班级学习委员被选中的条件下,两名数学科代表也被选中的概率;
(Ⅱ)在统计结果中,如果把《几何证明选讲》和《坐标系与参数方程》称为几何类,把《不等式选讲》称为代数类,我们可以得到如下2×2列联表:(单位:人)
|
几何类 |
代数类 |
总计 |
| 男同学 |
16 |
6 |
22 |
| 女同学 |
8 |
12 |
20 |
| 总计 |
24 |
18 |
42 |
据此判断是否有95%的把握认为选做“几何类”或“代数类”与性别有关?
下面临界值表仅供参考:
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式:K
2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
.



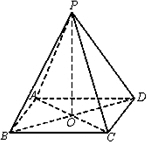 如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O.