
分析 (1)利用两角和公式和诱导公式对原等式整理可求得tanA的值,进而取得A.
(2)根据正弦定理表示出b和c,求得b+c的表达式,化简整理,根据正弦函数的性质求得其最大值,结合两边之和大于第三边求得范围.
解答 解:(1)由条件结合诱导公式得,sinAcos$\frac{π}{6}$+cosAsin$\frac{π}{6}$=2cosA,
整理得sinA=$\sqrt{3}$cosA,
∵cosA≠0,
∴tanA=$\sqrt{3}$,
∵0<A<π,
∴A=$\frac{π}{3}$;
(2)由正弦定理得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{6}{{sin\frac{π}{3}}}=4\sqrt{3}$,
∴$b=4\sqrt{3}sinB$,$c=4\sqrt{3}sinC$,
∴$b+c=4\sqrt{3}(sinB+sinC)=4\sqrt{3}[{sinB+sin(\frac{2π}{3}-B)}]$=$4\sqrt{3}({\frac{3}{2}sinB+\frac{{\sqrt{3}}}{2}cosB})=12({\frac{{\sqrt{3}}}{2}sinB+\frac{1}{2}cosB})$=$12sin({B+\frac{π}{6}})$,
∵$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,
∴$6<12sin({B+\frac{π}{6}})≤12$,即6<b+c≤12(当且仅当B=$\frac{π}{3}$时,等号成立)
点评 本题主要考查了正弦定理的运用,两角和公式的运用.考查了学生综合运用知识的能力和一定的运算能力.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
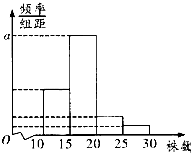 某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30) | 1 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $-\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{{4\sqrt{2}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com