
分析 (1)m=0时,f(x)=x|x|=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,接下来可以用函数单调性的定义进行证明:设x1,x2∈R,且x1<x2,分别在x1,x2都大于零或都小于零、或其中一个大于零另一个小零情况下得到f(x1)<f(x2),所以函数为R上的增函数;
(2)先在(0,+∞)上将原函数变形,变为f(x)=x|x-a|=|x(x-a)|,再令g(x)=x(x-a),通过讨论二次函数g(x)的性质可知,得到它的单调性:f(x)在(0,$\frac{1}{2}$a)上递增,在($\frac{1}{2}$a,a)上递减,在(a,+∞)上递增.再讨论自变量1究竟落在哪一个区间内,结合比较f(1)、f($\frac{1}{2}$a)的大小,再解相关的不等式,最后综合可得实数a的取值范围是[2$\sqrt{2}$-2,2].
解答 解:(1)证明:由题意,f(x)=x|x|=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,
任取x1,x2∈R,且x1<x2,
当0≤x1<x2时,f(x1)-f(x2)=x12-x22<0;
当x1<x2≤0时,f(x1)-f(x2)=-x12+x22=|x2|2-|x12|<0;
当x1<0<x2时,f(x1)-f(x2)=-x12-x22<0.
综上所述,f(x)在的上为单调增函数.
(2)在区间(0,+∞)上,函数f(x)=x|x-a|=|x(x-a)|,
令g(x)=x(x-a),它在(0,$\frac{1}{2}$a)上递减,在上($\frac{1}{2}$a,+∞)递增,
而在[0,+∞)上,f(x)=$\left\{\begin{array}{l}{g(x),x≥a}\\{-g(x),0≤x<a}\end{array}\right.$,
根据二次函数g(x)的性质可知,f(x)在(0,$\frac{1}{2}$a)上递增,在($\frac{1}{2}$a,a)上递减,
在(a,+∞)上递增;
当1∈(0,$\frac{1}{2}$a]时,即当$\frac{1}{2}$a≥1时,[f(x)]max=f(1)=a-1,解得a-1=$\frac{1}{4}$a2,
故此时a=2;
当1∈($\frac{1}{2}$a,a]时,即1≤a<2时,此时,[f(x)]max=f($\frac{1}{2}$a)=$\frac{1}{4}$a2,
此时的$\frac{1}{2}$a均满足题意.
当1∈(a,+∞)时,即0<a<1时,[f(x)]max为f(1)与f($\frac{1}{2}$a)中较大者,
而故f($\frac{1}{2}$a)=$\frac{1}{4}$a2,f(1)=1-a,故[f(x)]max=$\frac{1}{4}$a2,
当且仅当$\frac{1}{4}$a2≥1-a,解这个不等式,得2$\sqrt{2}$-2≤a<1.
综上所述,实数m的取值范围是[2$\sqrt{2}$-2,2].
点评 本题以含有绝对值的函数为例,考查了二次函数的单调性和函数的零点等知识点,属于难题.解题时应该注意分类讨论和转化化归等常用数学思想的运用.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
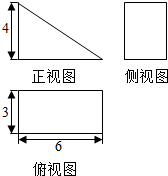
| A. | 36 | B. | $54+6\sqrt{13}$ | C. | $54+12\sqrt{5}$ | D. | $30+6\sqrt{73}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
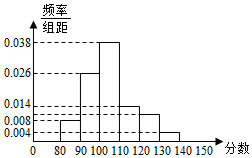 某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)
某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | x | 0.1 | 0.2 | 2x | 0.1 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com