Question

8．将底边长为2的等腰直角三角形ABC沿高线AD折起，使∠BDC=60°，若折起后A、B、C、D四点都在球O的表面上，则球O的体积为$\frac{7\sqrt{21}}{54}π$．

Answer 1

分析 通过底面三角形BCD求出底面圆的半径DM，判断球心到底面圆的距离OM，求出球O的半径OD，即可求解球O的体积．

解答 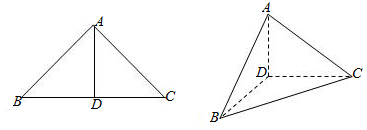解：如图，在△BCD中，BD=1，CD=1，∠BDC=60°，
底面三角形BCD的外接圆圆半径为r，则$\frac{1}{sin6{0}^{0}}=2r$
∴$r=\frac{1}{\sqrt{3}}$
AD是球的弦，DA=1，
∴OM=$\frac{1}{2}AD=\frac{1}{2}$
∴球的半径R=OD=$\sqrt{\frac{1}{3}+\frac{1}{4}}=\sqrt{\frac{7}{12}}$，
∴球O的体积为$\frac{4}{3}π{R}^{3}$=$\frac{7\sqrt{21}}{54}π$．
故答案为：$\frac{7\sqrt{21}}{54}π$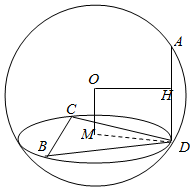

点评 本题考查球的体积的求法，球的内接体，考查空间想象能力以及计算能力．属于中档题．