
 ��֪��F��������y2=2px�Ľ��㣬����p������������M������Ϊ��12��8������N���������ϣ�������$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$��OΪ����ԭ�㣮
��֪��F��������y2=2px�Ľ��㣬����p������������M������Ϊ��12��8������N���������ϣ�������$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$��OΪ����ԭ�㣮���� ��1��������֪�������p�����ɵõ������ߵķ��̣�
��2����ֱ��AB�ķ���Ϊy=kx-k��A��x1��y1����B��x2��y2��������ֱ���������߷��̣�����Τ�ﶨ�����ֱ�ߵĴ�ֱ��ϵ����������ε��������ʽ�����û�������ʽ��⼴�ɣ�
��� �⣺��1����$\overrightarrow{ON}=\frac{3}{4}\overrightarrow{OM}$����N��9��6����
�е�N���������ϣ�36=18p��
���p=2��
���Ը������ߵķ���Ϊy2=4x������4�֣�
��2���������ֱ��AB��CD��б�ʶ������Ҳ�Ϊ�㣬
��F��1��0������ֱ��AB�ķ���Ϊy=kx-k��A��x1��y1����B��x2��y2����
��$\left\{\begin{array}{l}{y=kx-k}\\{{y^2}=4x}\end{array}$��ȥx�ã�k2x2-��2k2+4��x+k2=0��${x_1}+{x_2}=2+\frac{4}{k^2}$��x1x2=1���١���6�֣�
��AB��CD����$-\frac{1}{k}$������ʽ�е�k��ͬ���ɵã�${x_3}+{x_4}=2+4{k^2}$��x3x4=1�ڣ�����8�֣�
${S_{��AFC}}+{S_{��BFD}}=\frac{1}{2}|AF||CF|+\frac{1}{2}|BF||DF|$=$\frac{1}{2}��{x_1}+1����{x_3}+1��+\frac{1}{2}��{x_2}+1����{x_4}+1��$=$\frac{1}{2}��{x_1}{x_3}+{x_2}{x_4}+{x_1}+{x_2}+{x_3}+{x_4}+2��$����10�֣�
���٣��ڴ��룬�ɵ�${S_{��AFC}}+{S_{��BFD}}=\frac{1}{2}��\frac{1}{{{x_2}{x_4}}}+{x_2}{x_4}+6+\frac{4}{k^2}+4{k^2}����8$�������ҽ���k=1����${x_2}=3-2\sqrt{2}��{x_4}=3+2\sqrt{2}$ʱ����=��������
��S��AFC+S��BFD����Сֵ��8������12�֣�
���� ���⿼��ֱ���������߷��̵�Ӧ�ã���������ʽ��Ӧ�ã������߷��̵����������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��F1��F2����Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������ҽ��㣬������Բ��һ��P����|PF2|=|F1F2|����ԭ��O��ֱ��PF1�ľ��벻����b����������e��ȡֵ��Χ�ǣ�������
��F1��F2����Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������ҽ��㣬������Բ��һ��P����|PF2|=|F1F2|����ԭ��O��ֱ��PF1�ľ��벻����b����������e��ȡֵ��Χ�ǣ�������| A�� | ��$\frac{1}{3}$��$\frac{{\sqrt{2}}}{2}$] | B�� | ��0��$\frac{5}{7}$] | C�� | [$\frac{5}{7}$��1�� | D�� | ��$\frac{1}{3}$��$\frac{5}{7}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 95 | B�� | 100 | C�� | 99 | D�� | 90 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
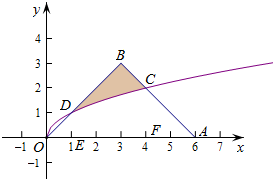 ��ͼ������������OAB�Ķ���A��B������ֱ�Ϊ��6��0������3��3������AB������y=$\sqrt{x}$���ڵ�C���ڡ�OAB����ȡһ��P�����P������Ӱ���ֵĸ���Ϊ��������
��ͼ������������OAB�Ķ���A��B������ֱ�Ϊ��6��0������3��3������AB������y=$\sqrt{x}$���ڵ�C���ڡ�OAB����ȡһ��P�����P������Ӱ���ֵĸ���Ϊ��������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{5}{27}$ | D�� | $\frac{11}{54}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com